The first step is to solve each of the triangular logic puzzles. The blue diamond icons and brown words can be ignored while solving the puzzles.
Note: In the solutions below, diamonds whose binary assertions are true are colored blue, and false ones are colored red.
| Puzzle |
Solution |
Author |
| Balance Loop |
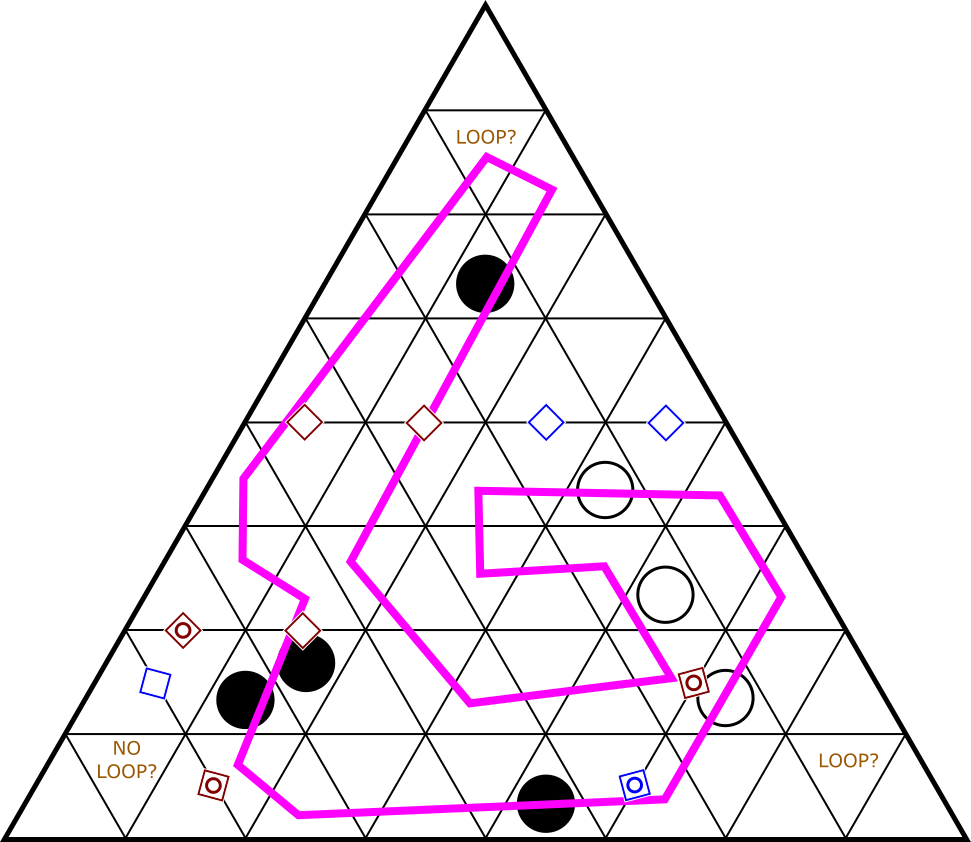
|
Shai Nir Hana |
| Corral |
|
Shai Nir Hana |
| Filliamond |

|
Shai Nir Hana |
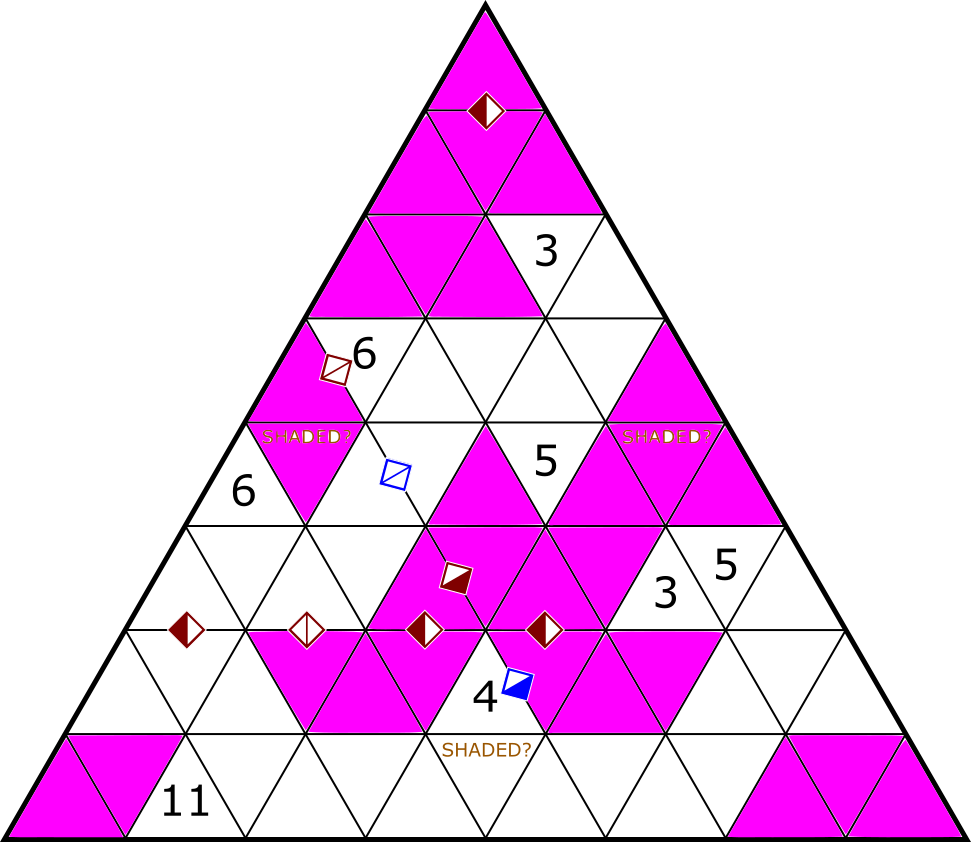
| Heyawake |
|
Matthew Schulz |
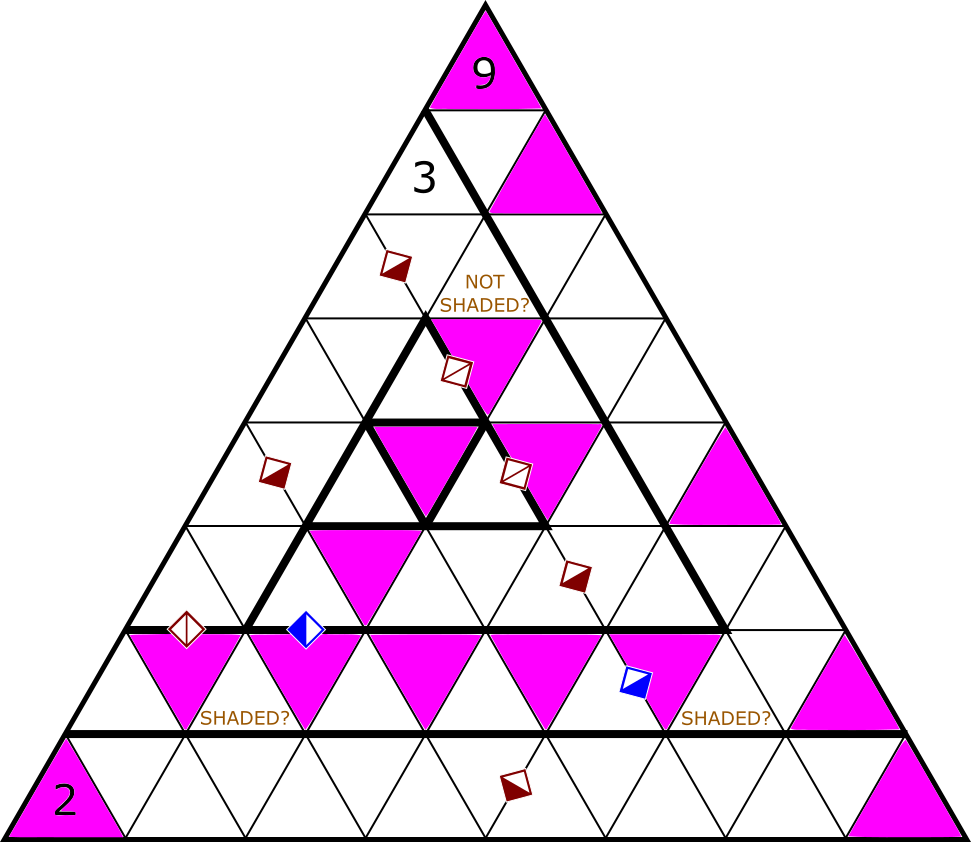
| Hidato |
|
Shai Nir Hana |
| LI |
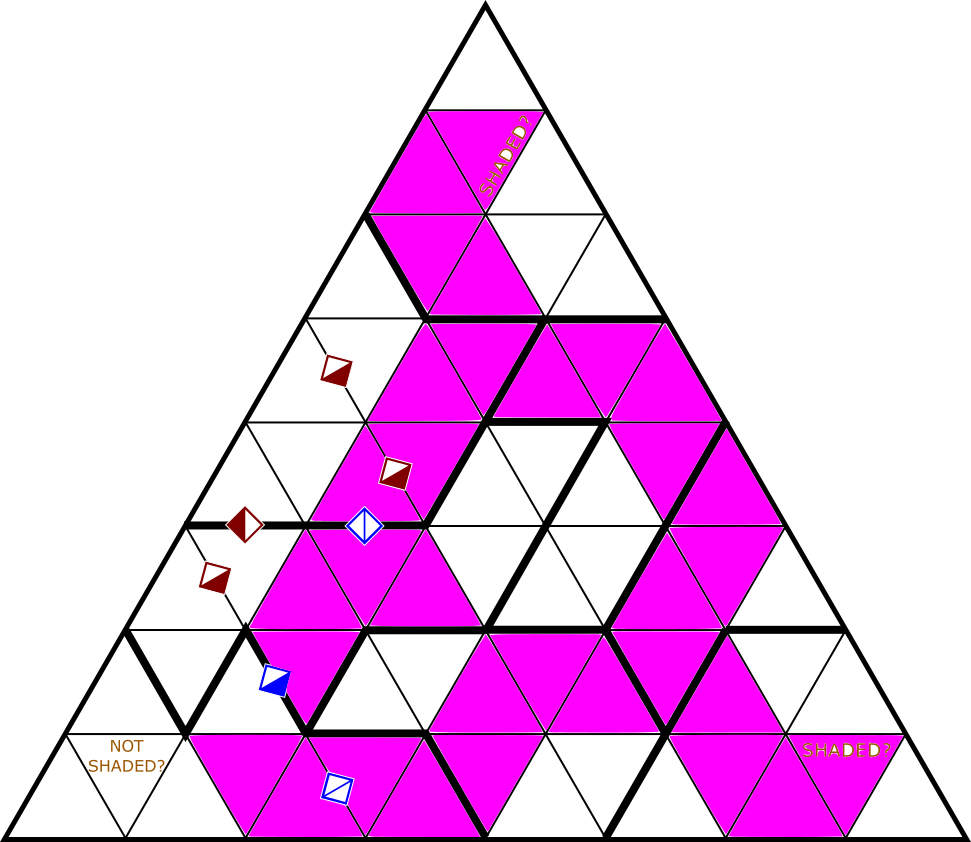
|
Shai Nir Hana |
| Loop and Block |
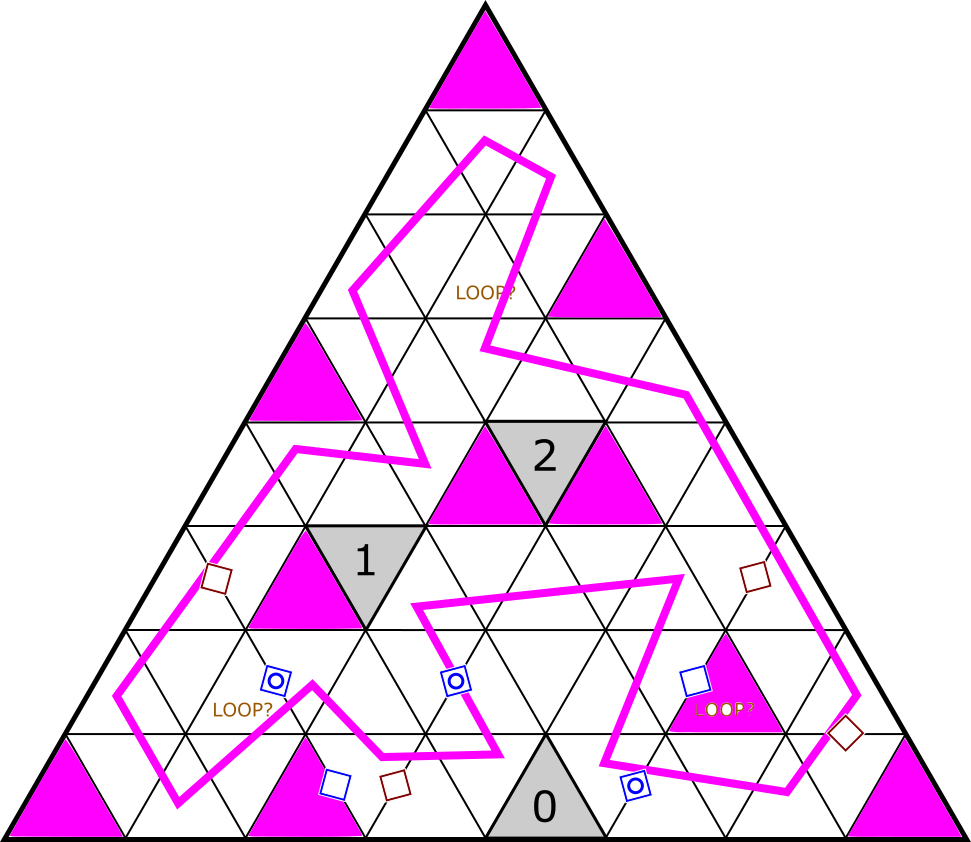
|
Daniel Hunt |
| Moon-or-Sun |
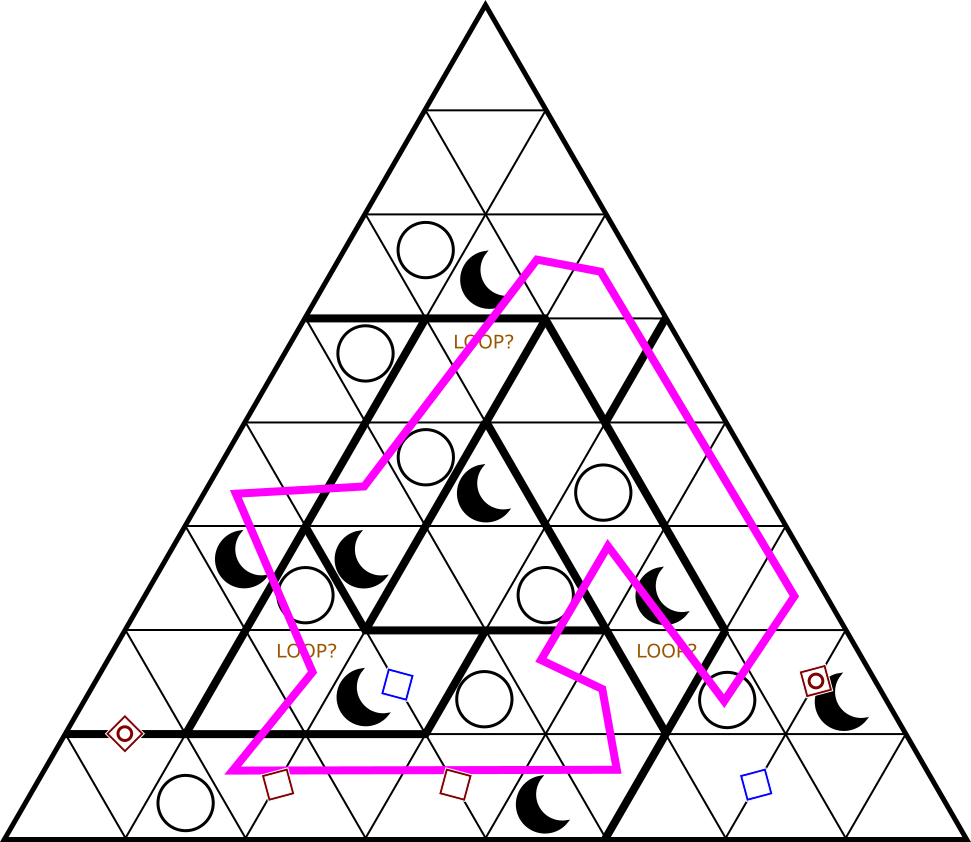
|
Celestine Lau |
| Nonogram |
|
Shai Nir Hana |
| Pentiamondous |
|
Shai Nir Hana |
| Slitherlink |
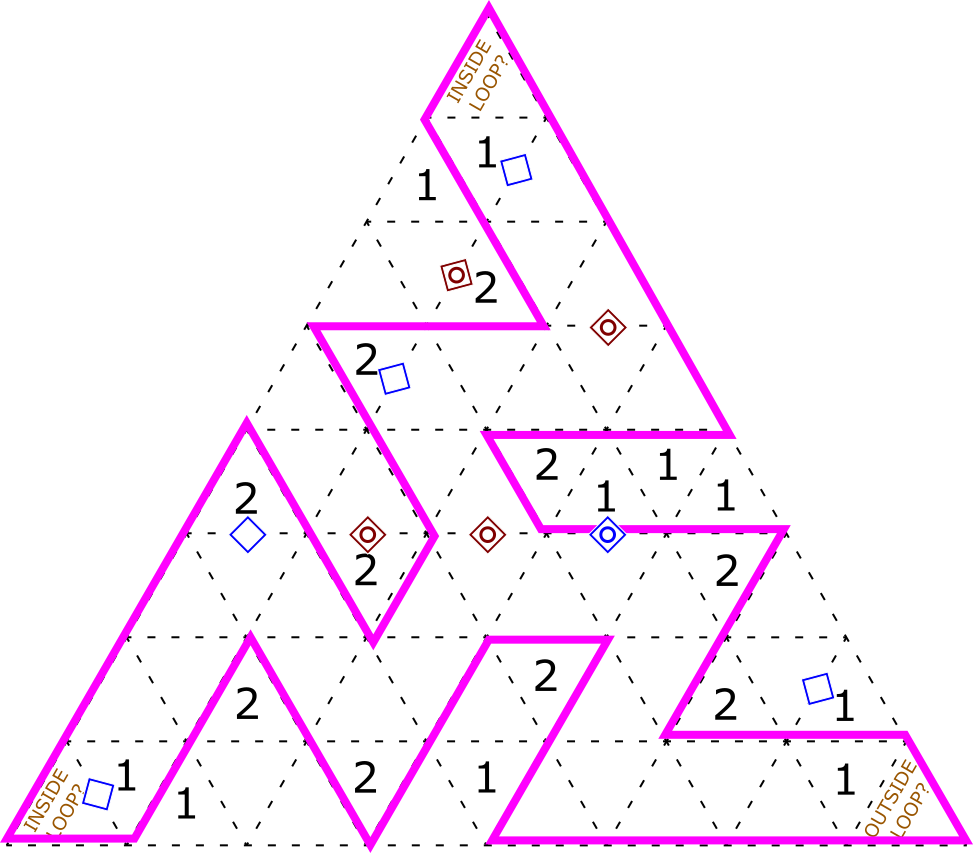
|
Kah Kien Ong |
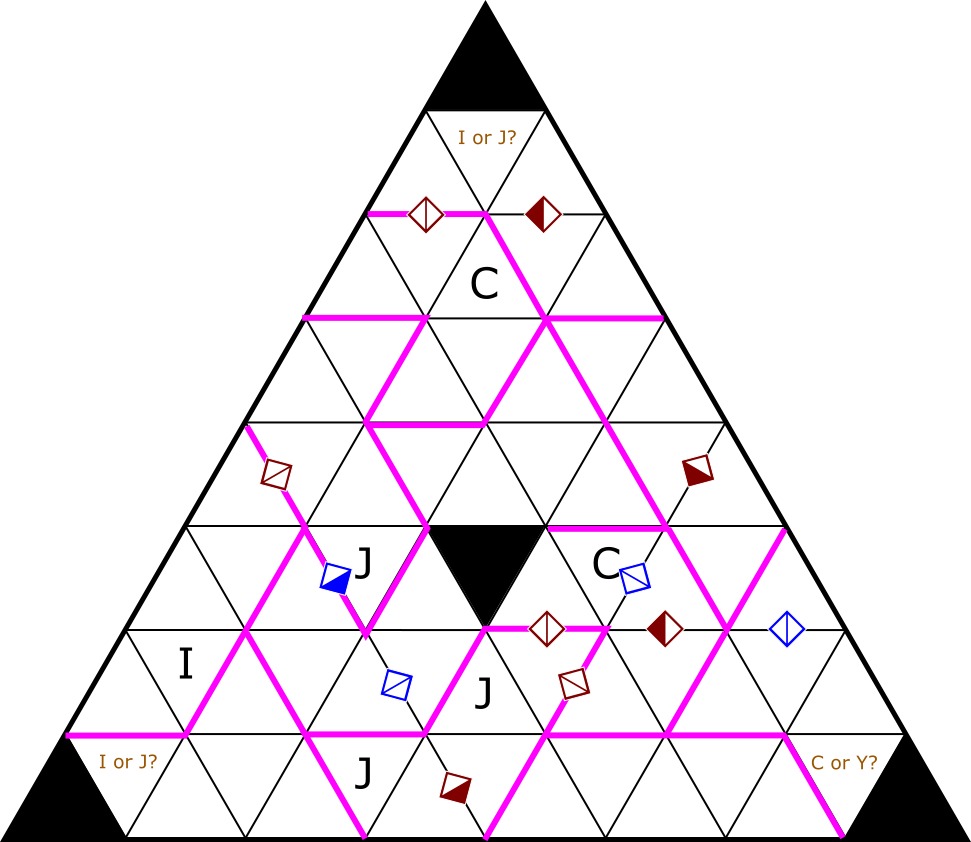
| Snake |
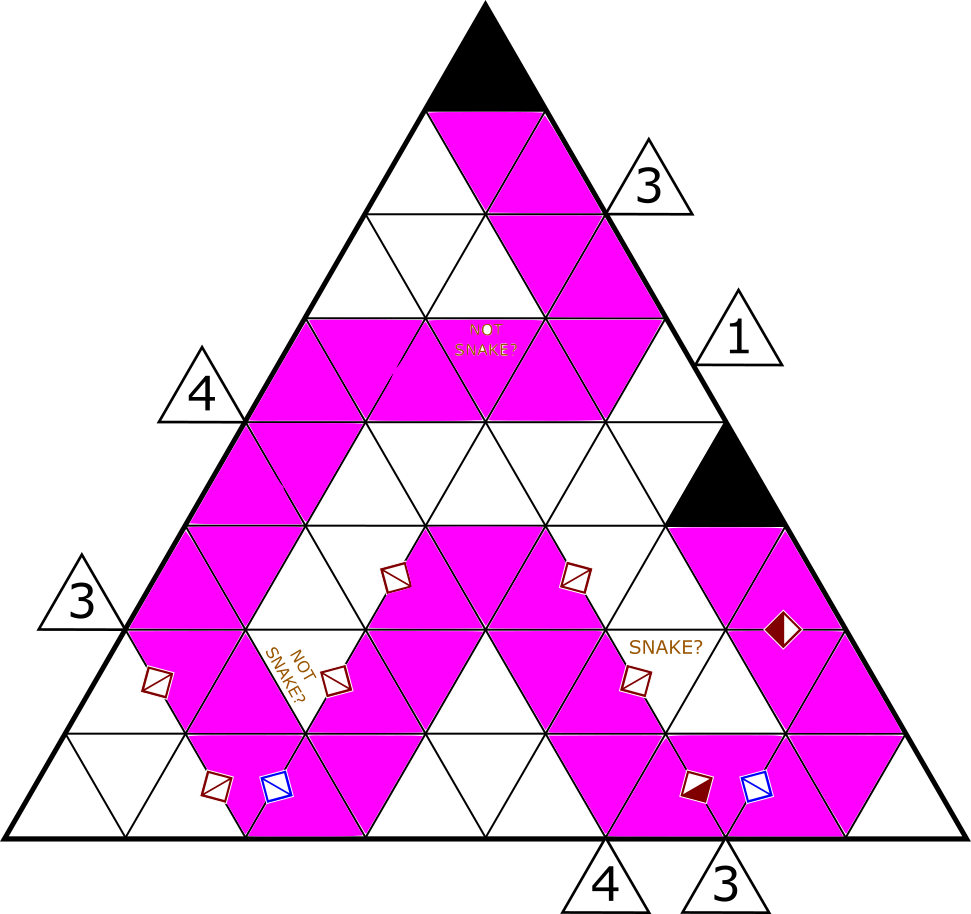
|
Daniel Hunt |
| Statue Park |
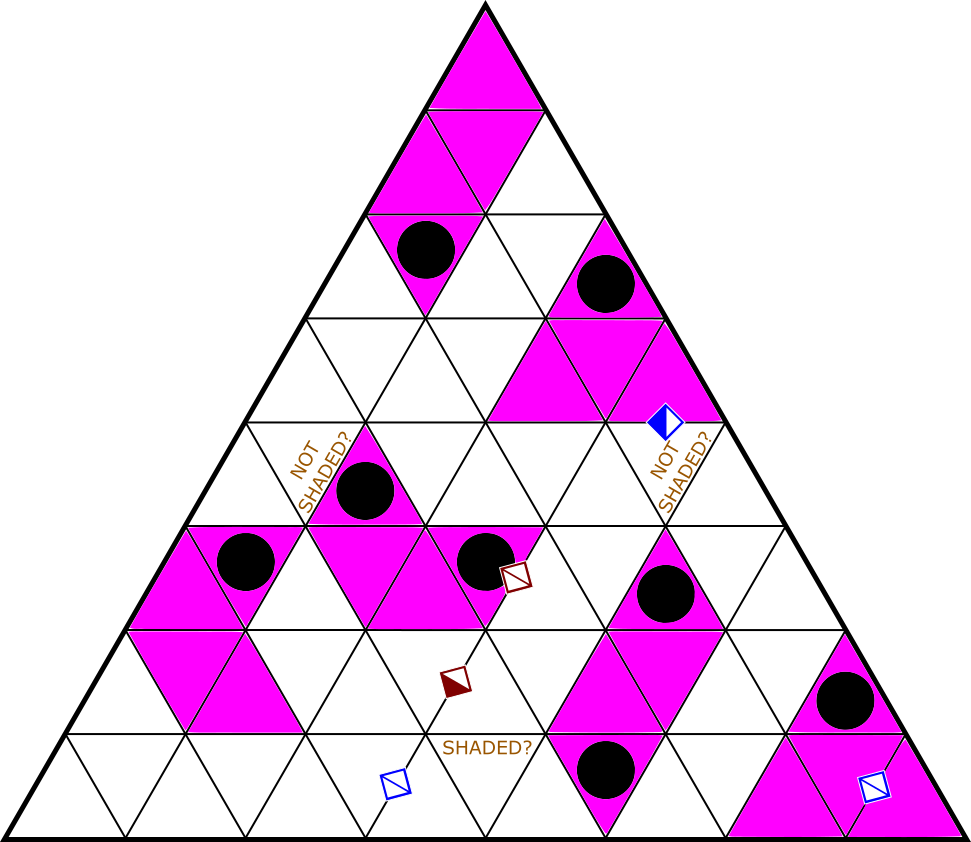
|
Shai Nir Hana |
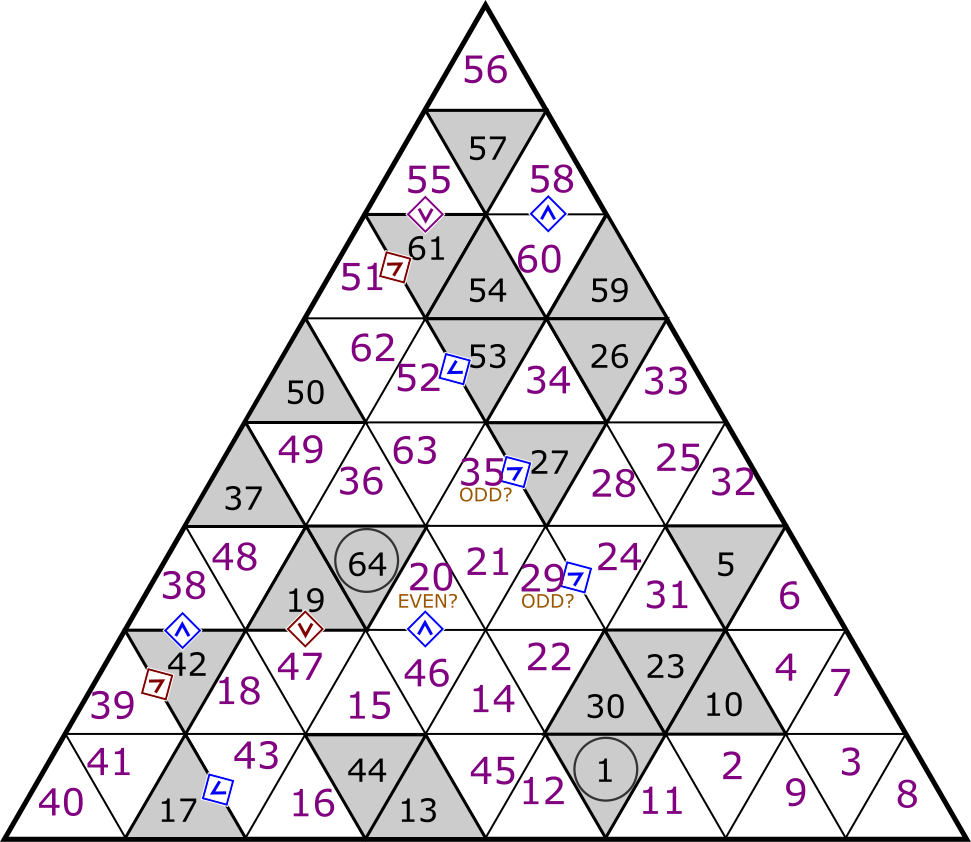
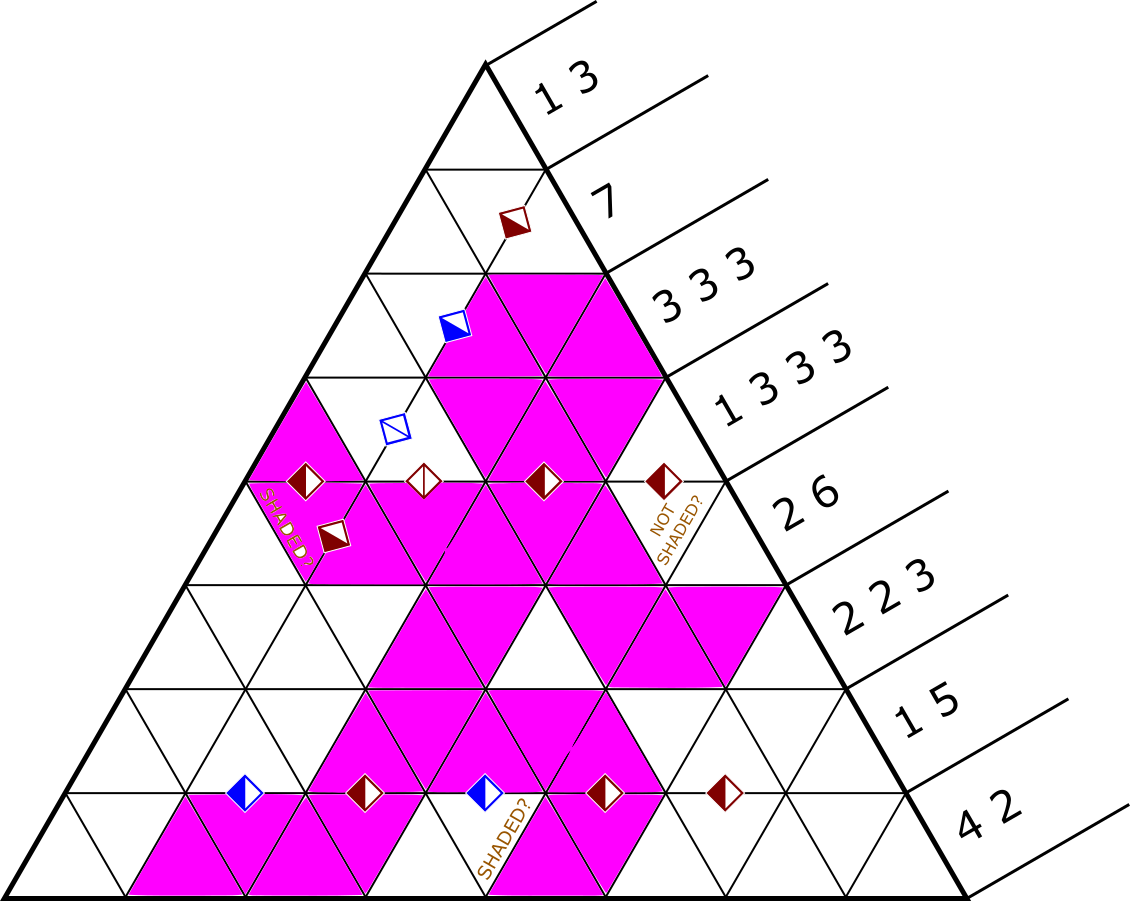
Note the first image in the key on the last page: It’s a shape with 13 triangles. We’re going to be assembling the 13 puzzles into one big grid with that shape, and orienting it such that the direction indicated by the arrow (only present on Filliamond, the center triangle) is pointing up.
The presence of binary statements, as well as the flavor text (“bit by bit by bit by bit by bit”), suggests we should try to read data as binary. There are a couple of 5-length segments of diamonds in the puzzle, and every other row of diamonds is shorter and hits the edge of its grid. We can assemble all of the grids together such that every diamond is part of a 5-length segment, which we can then read according to the order specified in the image on the second row of the key (with 1a, 1b, and 2):
With our heads turned for each direction, reading from top to bottom, the letters read:
| 1a |
ALLVOWELS |
| 1b |
AREFLAT |
| 2 |
LASTNAME |
Finally, the only part of the puzzle we haven’t yet used are the brown questions that are on 3 cells in each puzzle, and the similarly colored diagrams at the bottom of the key. The diagram indicates how we can order the binary answers on the cells to get 3-digit binary numbers. Those can only represent the letters A through G, which is all we need, because we are going to interpret them as musical notes (clued by “flat” in the extracted phrase and by “music” in the flavor text). In particular, As and Es are all flat (musically inclined solvers may notice that, as long as there are no Bs — which is the case in this puzzle — this can represent a valid musical key). When extracted from the fully assembled diagram, preserving the rotation of each grid from the previous step, we get the following notes:
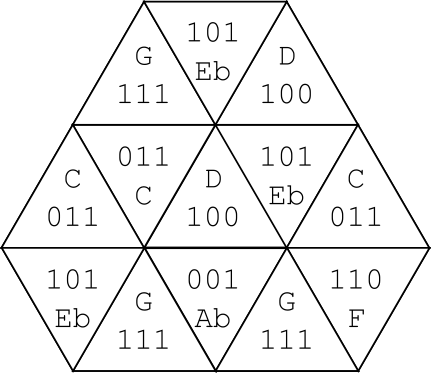
G E♭ D C C D E♭ C E♭ G A♭ G F
You might play this and recognize the tune, or input the notes into a music search engine like Musipedia. The famous musical piece that has this phrase is “Waltz No. 2,” and its composer’s name is Dmitri SHOSTAKOVICH, which is the answer.
Author’s Notes
Waltz No. 2 is one of Shostakovich’s most famous works, and the whole idea for this puzzle came from the concept of a waltz: Taking something that’s usually in 4-count, and doing it in 3-count instead. I considered using ternary code for maximum 3 theming, but binary felt like a more elegant representation for the letters A through G, and — most importantly — made it really easy to put any binary condition on any cell or edge. This allowed the extraction piece to be written completely independently of the puzzle logic, which could then be distributed among multiple authors with minimal fuss.
Some puzzle types translated readily to triangle forms. Others took some trial and error to figure out the exact translation of the rules (for example, what the triangular equivalent of the “no 2x2” rule from LITS was going to be). I spent far too many hours of my life trying to get Skyscrapers to work in triangular form, but it ended up being exceedingly difficult.
Shout-out to the Pyramid Cult's Favorites puzzle series, which provided some of the few examples of how triangular versions of puzzles might work.
There was a Spiral Galaxies puzzle kept around as a backup in case something went terribly wrong with one of the mini-puzzles during playtesting. It was never needed, but you can try it here (standard Spiral Galaxies rules; galaxies may have either 180-degree or 120-degree rotational symmetry).
Notes for individual mini-puzzles:
-
Balance Loop: The instructions for this could have been just “standard Balance Loop rules” except for how unintuitive it is to think about turns in the triangular world.
-
Filliamond (and Pentiamondous): Polyforms made of triangles are called “polyiamonds” and so I couldn’t get myself to call these “Fillomino” and “Pentominous,” even if it would have made them easier to pronounce.
-
Heyawake: There is apparently a split in the Heyawake fandom over whether the precise rule is that a line of white cells can include at most two regions or at most one border.
-
Hidato: As an Israeli, I felt like I had to at least try to include my native country’s contribution to the canon of logic puzzles. I settled on this adjacency rule after trying “must share a vertex,” which was too loose to allow for satisfying logic, and “must share an edge or be opposite on a vertex,” which was too restrictive.
-
LI: This one could probably have been interpreted a few different ways. I could imagine rule sets that use the A tetriamond either as an allowed shape along with L and I, or as a forbidden shape analogous to the O tetromino in LITS. I think the minimalistic LI rules lent themselves to a nice, approachable puzzle, though.
-
Loop and Block: Daniel submitted this when we already had 13 puzzles, but I liked the logic so much that I put it in and relegated Spiral Galaxies to a backup.
-
Nonogram: The working title for this one was “Monogram.” The reflect-off-the-wall mechanic was an attempt to counter the fact that some rows in a triangle have very few cells, meaning that clues along those rows would be less interesting. I drew the little dancing character just to play around and get a feel for how a one-sided Nonogram might behave, but the solve path turned out to be interesting enough that I decided to keep the image with no modification.
-
Pentiamondous: Placing pentiamonds in a triangle can actually be very restrictive. An earlier version had a unique solution with one fewer clue, but it needed so much branching logic to get the solution that the test solvers mutinied.
-
Slitherlink: The symmetrical solution is an abstract shape resembling a tri-legged brand logo (from the maker of a popular medicinal drink in South-East Asia).















