Solvers should cut out the pieces carefully, and then assemble them into a square.
They need to match up the gray and black heavy lines on the borders of the pieces, the small black circles, and the hairline borders (which go on the outside of the square), to form this:
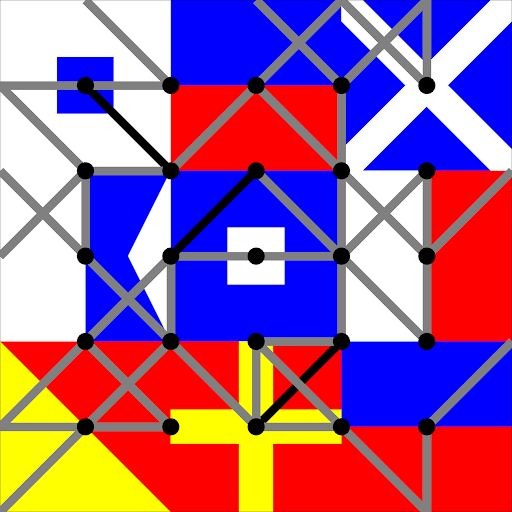
Behind the gray and black piece borders, solvers can see a 3×3 grid of international maritime signal flags, spelling out SEMAPHORE in row-major order.
Solvers need to interpret the gray and black piece borders as semaphore lines. Ignoring the signal flag images and placing a semaphore center point at each of the small black circles in the interior to the grid yields this:
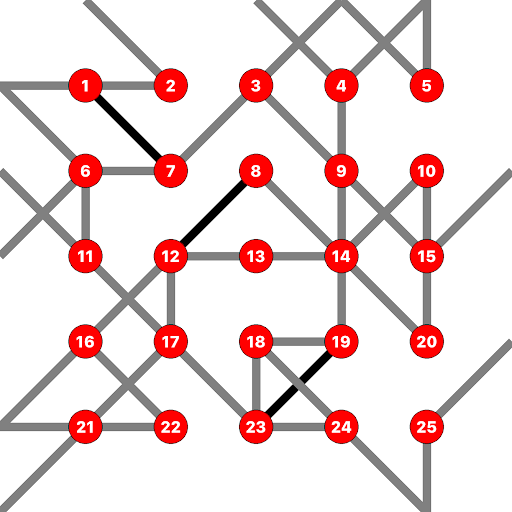
The semaphore lines extend all the way to the next grid point (or edge); sometimes diagonal lines will cross. A gray line indicates a single semaphore line (like from point three to point seven). A black line indicates two overlapping semaphore lines (like from point one to point seven and from point seven to point one).
Many points have more than two lines connecting to them, but it’s a pretty simple logic exercise to work out the unique pair of lines from a given point that form the semaphore symbol centered at that point.
We begin by noting that points 2, 5, 8, 10, 13, 20, 22, and 25 have only two connecting lines, so we can fix their semaphore symbols and remove the lines that connect to them:
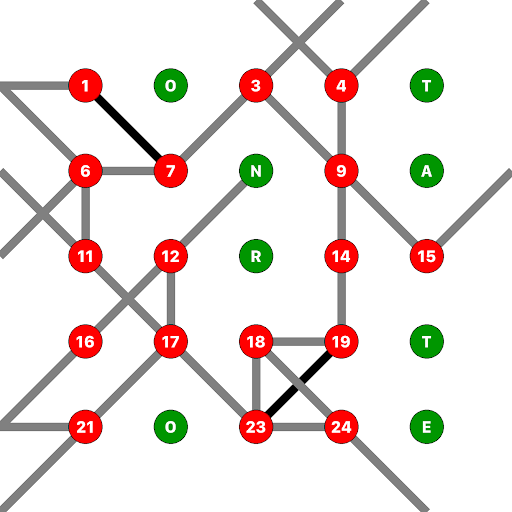
Continuing this logic, we can now fix points 1, 14, 15, and 16:
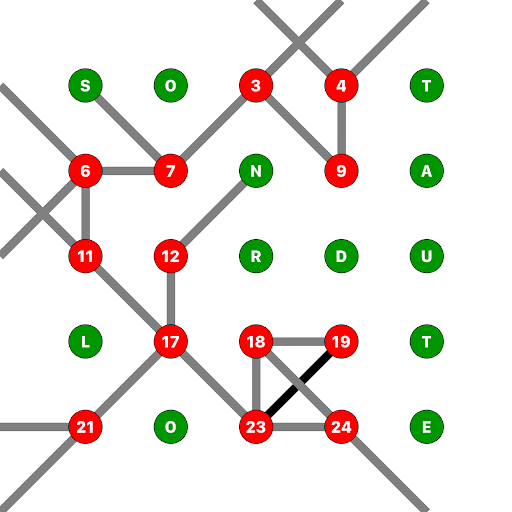
And now points 9, 12, and 19:
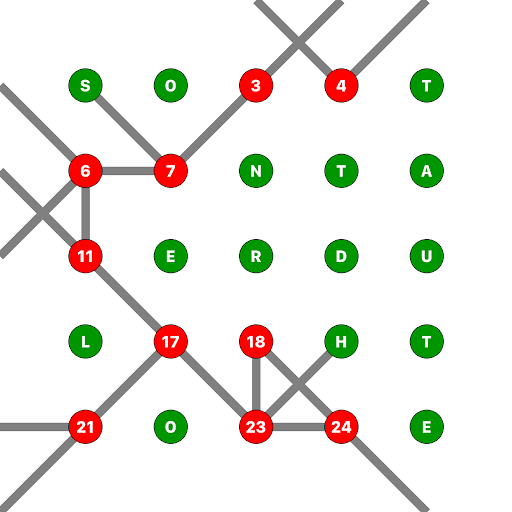
Then points 3, 4, and 18:
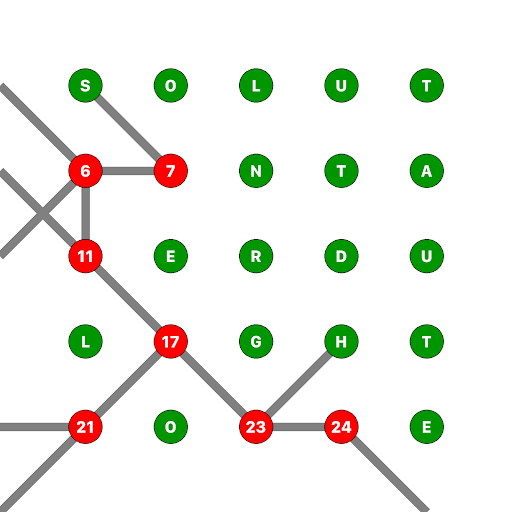
Next points 7, and 24:
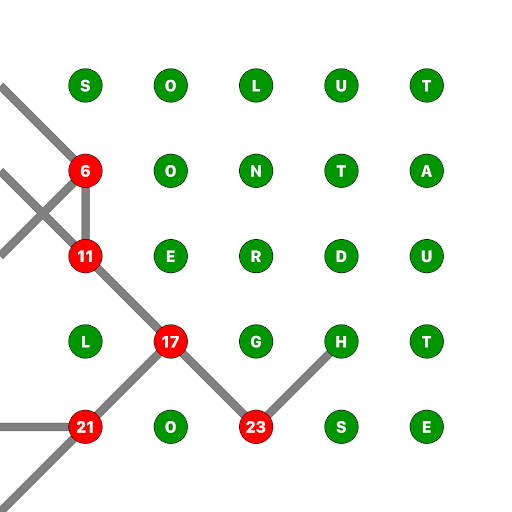
And finally, in sequence points 23, 17, 21, 11, and 6 to obtain:

From which we can read the message SOLUTIONTATERDULIGHTHOUSE, yielding the puzzle’s answer TATER DU LIGHTHOUSE (which is—duh!—a lighthouse. In Cornwall, England).