This puzzle consists of a set of 48 algebraic expressions, containing 48 unique symbols, as well as one numerical constant per expression. Each symbol, and each expression, correspond to one of the 48 continental United States. Each state’s expression uses exactly the symbols of the states geographically adjacent to that state, and the solver may eventually realize that within each expression, the states are referenced in alphabetical order—using these facts, we can uniquely match symbols and expressions to states.
States are considered adjacent when they share a land border. We consider the Four Corners states to be adjacent to one another. The algebraic expressions provide sufficient confirmation for solvers to be able to unambiguously resolve questionable adjacency scenarios.
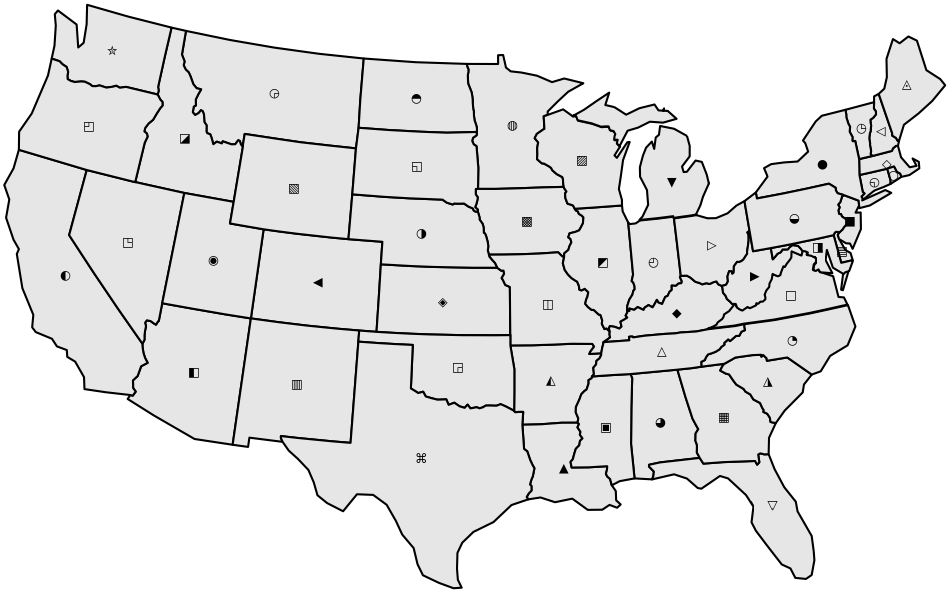
The next step is to assign an initial value to each state. The text “Our founding fathers started this nation from nothing” is intended to clue that the initial value assigned to each state should be zero.
We can now treat the algebraic expressions as transition functions from one “state” of state values to the next. During each transition, we replace a state’s value with a value computed from its geographically adjacent states, according to that state’s algebraic expression.
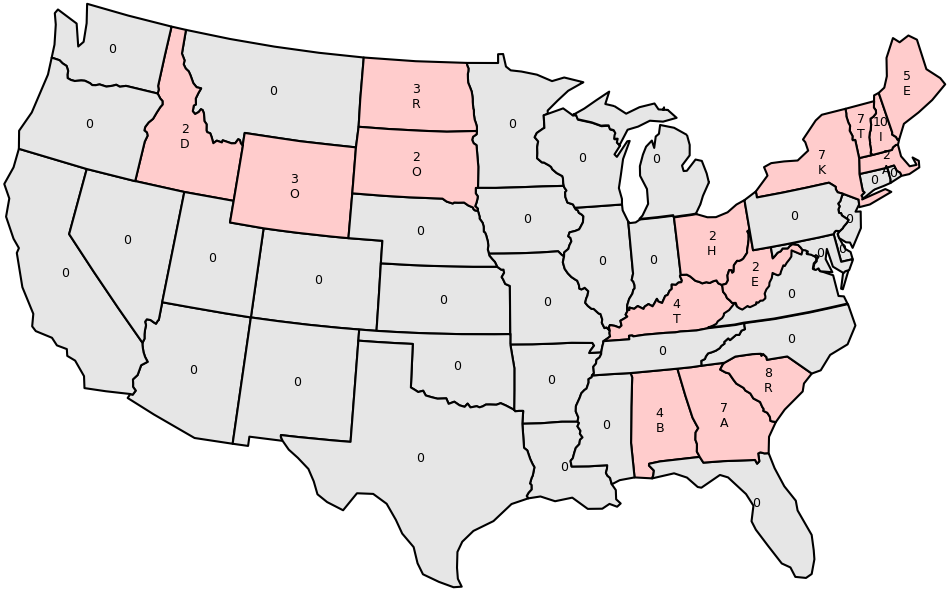
After repeating this process several times (it turns out that three iterations are needed to solve the puzzle), we reach a state where all values are either zero or positive. Indexing into state names using the positive values, and writing these letters in the locations of their states on the map, we can read a word from each cluster of states on the map and extract the answer phrase KATIE BAR THE DOOR.