The Western Union operator was just about to close up shop before the fireworks. “Please,” you cry, waving your scrawled note. “I need to wire this itinerary.” The operator grudgingly hands you a blank form and waits.
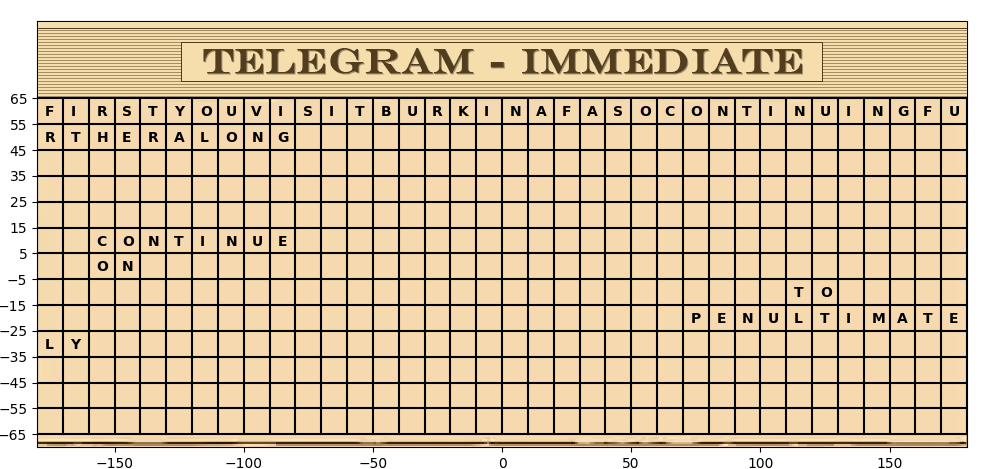
FIRST YOU VISIT BURKINA FASO CONTINUING FURTHER ALONG ? AND TO ? ZIPPING TOWARDS ? AND ? AND ? CONTINUING THEN DIRECTLY TO ? NEXT GO TO ? AND ? THEN ? AND CONTINUE TO ? THEN SCENIC ? ON TOWARD ? THEN TO ? AND GO ON TOWARDS ? AND ? TO ? NEXT VISIT ? AND PENULTIMATELY ? AND ? . . . . .
- Start in Burkina Faso.
- From its capital[1], go south 36 degrees. Travel in latitude until you reach a country[2] whose entire land area[3] is inside the convex hull[4] of another country’s capital territory[5].
- From its capital, follow a great circle initially heading north or south. For each contiguous territory[6] you encounter, draw the largest possible circle that contains only seawater and which lies within the territory’s convex hull, and draw the largest possible circle containing only land. Stop in the territory for which the water-circle radius is the largest fraction of the land-circle radius. (You should find yourself in a non-capital-territory where the large seawater circle did not touch the convex hull at all.)
- From its capital, find a capital territory at the same longitude whose land area can be bisected by the relatively shortest[7] straight line.
- From its capital, head east. Stop in the capital territory where the ratio of the longest overland road trip[8] to the longest great circle separation of two points in the same territory is largest.
- From its capital, among all the countries with any land territory 6004 km away, stop in the one which has land borders with only one other country (although it and a current non-land-border neighbor have a small sovereignty dispute which might be imagined to add a second land border someday.)
- From its capital, move along a path that takes you south 0.45 degrees of latitude for every 1 degree east in longitude. Examine the polygonal spaces between the convex hull of, and the actual border of, each contiguous territory. Stop in the country for which this exercise yields the largest perfect triangle[9]. (You should hit this territory with over 100 miles to spare, and miss the country whose protruding corner fills the triangle of interest.)
- From its capital, move along a path that takes you south 0.28 degrees of latitude for every 1 degree west in longitude. Stop in the only capital territory you encounter whose northernmost point is east of its southernmost point. (Both the northern and southern points of your goal are unambiguous. Slightly south of your path is a country whose northernmost point might move east or west of the southernmost depending on small changes in tidal mudflats.)
- From its capital, follow a great circle that also passes through Lake Issyk-Kul. Your destination is the capital territory along this route for which, when you draw the tightest possible circle that contains that territory, the territory’s land area is the smallest fraction (less than 15%) of that circle’s area.
- From its capital, follow a rhumb line that crosses longitudes at an angle of 15.90 degrees south of east. There is only one capital territory on this path that you will enter by land, exit by land, reenter by land, and exit by sea, in that order. In fact, you should enter and exit it again. (Once you find these conditions, check that you’re on one of the shallowest bearings that allow it. A path erring 1.5° too steep would behave as described but send you astray afterwards.) But don’t stop in that country—continue along this path and visit the very next country you reach.
- Explore the countries with land territory a distance 3586 km from its capital. Stop in the country which lies entirely within (although it’s a close call on one) the convex hulls of TWO different contiguous territories.
- From its capital, follow a great circle which also passes through the center of Adolphus Island in the Cambridge Gulf. This great circle passes through one exclave; go there.
- On an equirectangular map, draw a straight line through its capital which is tangent to the radius-3586 circle you drew in clue 11. Head southwest, ignoring your starting country and, if necessary, its neighbors. Stop in the first of the three countries on this route—you should hit its northwest corner—which have a relatively long (relative length > 0.2) border along a line of longitude.
- From its capital, head west along a great circle with initial heading 264.9°. For each capital territory on this path, construct a quadrilateral whose corners are the southernmost, westernmost, northernmost, and easternmost points of the territory. Restrict your attention to cases where the capital city lies outside, and specifically to the southwest of, this quadrilateral. Go to the country where the quadrilateral has the largest area relative to the capital territory’s area—indeed, you should find that the quadrilateral’s area and the country’s area are nearly equal.
- In its capital, check the magnetic declination (referencing WMM 2015). Head southeast until you find an isogonic line whose declination is 25 degrees further west. Follow that isogonic line towards the South Magnetic Pole and stop in the first country where you make land.
- From its capital, follow a great circle initially heading due north. This path passes through many countries but usually also passes through at least one land neighbor of each such country. Stop in the first country you enter which has no neighbors along this path.
- Inscribe a regular tetrahedron in the Earth with this country’s capital as one vertex. Place a second vertex on the west coast of the Antarctic Peninsula. Go to a sovereign nation whose exclusive economic zone, but not its land territory or territorial sea, contains another vertex. (The fourth vertex should be on or near the coast of a country not otherwise referenced in these instructions.)
- From its capital, follow a great circle with initial magnetic heading 240°. Ignoring islands, stop in the capital territory on this route whose land area fills the largest fraction of its smallest circumscribed circle. (Note that the route passes between two countries which are even more circle-filling.)
- From its capital, draw a circle of radius 13880 km. (You need four significant figures of that distance.) Look for contiguous territories touching this circle which are fairly long and narrow, with the longer axis more aligned with the arc of the circle and the narrower axis aligned with the radius, such that if the territory’s projection on the radial axis is of length B and its projection on the arc is of length A, then A/B > 3. Among such territories, visit the second-largest one by area.
- In its capital, you see the International Space Station fly directly overhead. One hour and 56 minutes ago it was over a different country, in principle visible from the capital; go there.
Footnotes
- [1] “Capital” always refers to a national capital. Amsterdam, Colombo, Dodoma, La Paz, Mbabane, Naypyidaw, Porto-Novo, and Pretoria are taken to be capitals.
- [2] A “country” is an independent state listed as such by the State Department. The “short form” is what we consider the name of a country, with the following exceptions: ROC and DRC take their long-form names; “Micronesia”; “North Korea”; “South Korea”; “The Bahamas”; “The Gambia”; “Vatican City”. Nothing in this trip is altered by the resolution one way or another of border disputes in Jammu and Kashmir, Arunachal Pradesh, the Spratly Islands, Crimea, or anywhere else we are aware of.
- [3] “Land area” is the area of contiguous territories, including lakes and rivers but ending at ocean/sea shorelines. The land area of Uganda includes much of Lake Victoria, but the land area of Greece does not include the Gulf of Corinth. The Caspian Sea and Black Sea are ocean-like for these purposes.
- [4] Unless otherwise specified, geometric constructions, lines, and polygon edges are always great circle segments.
- [5] A “capital territory” is the contiguous territory[6] containing the national capital. The capital territory of Denmark is Zealand, but not Jutland.
- [6] A “contiguous territory” is a unit of land bounded by international borders or oceans. Belfast is in a different contiguous territory than Dublin or London or even Ballyconagan. For this puzzle, unless otherwise instructed, you may ignore islands if they represent less than 5% of the country’s land area.
- [7] “relative distance”: A relative distance or length or is a geometric length scaled by the square root of the relevant territory’s area. The relative distance across the middle of a disc is 2/√π.
- [8] “overland road trip”: in the same sense that a convex hull could be generated by a rubber band stretched around the outside of a polygon, an overland road trip is the path of a rubberband between two points but constrained to fall within a polygon; it’s a distance as the crow flies, if the crow could not cross borders or saltwater.
- [9] “perfect triangle”: This is an exception to footnote [4]. A perfect triangle in this case may be any combination of great circle arcs, lines of latitude, or other lines that basically look straight on a map because let’s face it this triangle is a lot smaller than the curvature of the Earth so let’s not be sticklers about it.