Hall of Archaeology

This puzzle is all about using minesweeper-ish rules for different types of grid logic puzzles. Minesweeper has an interesting mechanic where we reveal the puzzle as we solve it, and that progress often involves knowing a cell is “safe” to reveal without necessarily knowing what we’ll see when we do reveal it. That same principle gives some interesting new ways of thinking about other classic puzzle types.

After each grid is solved (not counting the practice grid) we get a message unearthing a “masterfind” with some number of white and black pegs. Within each dig site, these form a mastermind puzzle, each of which is solved independently of the other dig sites. The three dig sites together provide the three-word solution.

Dig site 1:

CYPRUS - 1 black, 2 white

NUTMEG - 1 black, 2 white

COSWIG - 2 black, 1 white

MALTOL - 2 black, 1 white

There are 12 pegs total but no individual letter is used more than twice across the four words, so each correct letter must appear exactly twice - the only candidates are C,G,L,M,O,S,T,U. With trial-and-error we quickly find that the right set and only possible placement is CUSTOM.

Dig site 2:

ATI - 0 black, 2 white

LAF - 0 black, 1 white

ILA - 0 black, 1 white

The A is a red herring; there can’t be an A in the solution because there are no black pegs. ATI implies we need an I and T, ILA now tells us there’s no L, so LAF gives us an F; the answer is FIT.

Dig site 3:

OLPE - 0 black, 3 white

CODE - 1 black, 0 white

DECO - 1 black, 0 white

The only way to reconcile CODE and DECO having one black peg each is that one of those four letters must be used twice. Using an E would be impossible, so our letters are O,O,L,P, and the answer is POLO.

The final answer is CUSTOM FIT POLO.

Appendix

Here are some notes on how to approach each individual puzzle. In general, progress on these puzzles is made by identifying a cell that must be safe, clicking it, and using the newly revealed information to make the next deduction.

Battleships

After flagging every cell (except the given ship) in rows 7 and 8, focus on R5C3. It’s impossible to fit 8 ship parts total into columns 3 and 4 without one of those ship parts being in R5C3.

Masyu

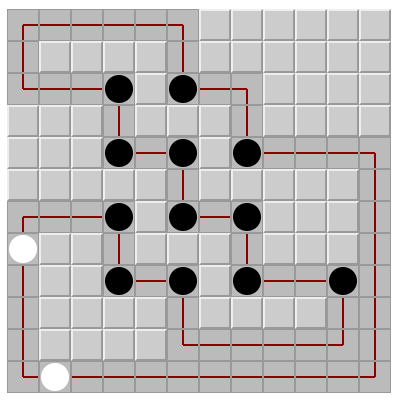
Start by filling the path along the bottom edge of the grid, and also horizontal line segments at R5C5 and R7C7. Next R8C4 can’t be empty, or there’d be no way to connect the lower three black circles to the rest of the loop.

Hashiwokakero

Start by drawing the bridges down from the upper-left 3, then the uncovered 4, the 3 at R3C6, and the 2 at R1C7. At this point R7C2 can’t be empty, or the diagonally adjacent 3s won’t both have room to escape that corner.

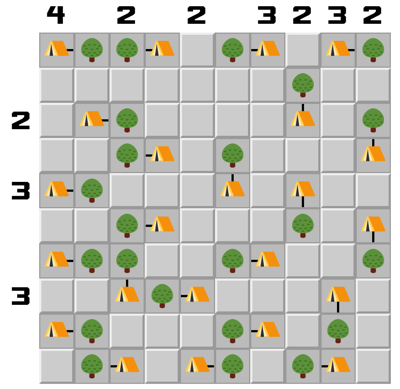
Tents

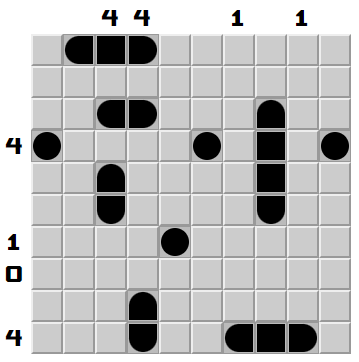
Two tents can be found right away in column 3; rows 8 and 10. Next focusing on column 1, we should be able to tell there’s a tent either in row 9 or 10. So R9C1 is therefore safe to click on - it either has a tent, or it has a tree from a tent at R10C1.

Fillomino

What’s in R4C1? Not a 2, obviously. If it’s a 1, then R4C2 is safe to click on. If it’s anything bigger than 2, R4C2 is still safe to click on.

Skyscrapers

The top three rows with 6 visible skyscrapers have to have the numbers 1 through 6 consecutive and in order. So the middle cells in those three rows are all safe to click on, and the top three rows can be finished from there.

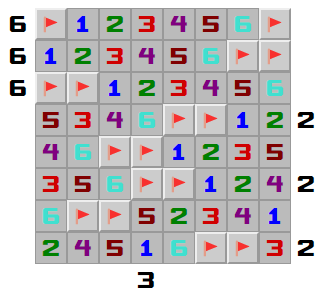
Easy As ABC

In columns 2 and 3, the As have to be in the bottom three rows. Therefore the top four As are in columns 1, 4, 5, 6 in some order. That pins the row 8 A to R8C8, the row 5 A to R5C7, and row 6 columns 2 and 3 are both safe to click.

Slitherlink

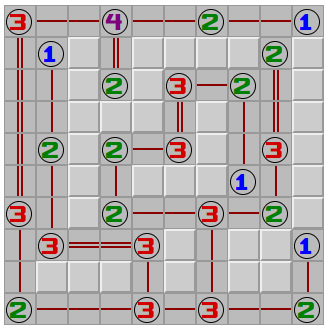
R11C11 is a good place to start - the region has to extend east from there, any other option quickly leads to a contradiction.

Nurikabe

It’s safe to click on R9C13 or we’d end up with a 2x2 region filled with ocean. Once that 13 is revealed it has to join with the 13 at R15C8, but the 9 and 12 in the bottom right will require as much space as the 13 region can give.

Norinori

Break into the puzzle by realizing R10C8 can’t be empty, and then R11C9. Once we find out that the bottom-middle 1x6 region has two domino halves instead of a whole domino, we can conclude the same is true for all the other 1x6 regions in the grid.

Authors' Notes

This puzzle was inspired in part by a very cool group round in the 2017 World Puzzle Championship hosted by India, which implemented the minesweeper concept by using scratch-off paper. If you thought a cell was safe to “click” on, you could scratch it off to either reveal information or a smiley face letting you know you’d messed up.