Junky Logic
In this interactive puzzle, each cell can be "correct" or "wrong", depending on how the grid is shaded. The rule for each cell is determined by its letter. By playing around with the grid, we can uncover these rules.
| Letter | Rule (regions are orthogonally connected components) |
|---|---|
| A | Region doesn't touch the border |
| B | Sees exactly 4 cells horizontally or 4 cells vertically |
| C | Sees the border |
| D | All diagonally adjacent cells are shaded |
| E | Shaded |
| F | All F's are in the same region |
| G | Region is rotationally symmetric |
| H | Even number of shaded in row |
| I | Not in a 1x3 |
| J | In the bend of a J-tetromino |
| K | Bottom left cell of a 2x2 checkerboard |
| L | Region touches the border |
| M | Sees exactly 4 cells |
| N | Exactly 2 N's in region |
| O | Not a singleton region |
| P | Exactly 5 shaded cells in 3x3 neighborhood |
| Q | No shaded 2x2 globally |
| R | Odd number of shaded in row |
| S | Exactly 1 neighbor with same shading as itself |
| T | Exactly 3 shaded among neighbors and itself |
| U | Unshaded and cell to the right shaded |
| V | Exactly 2 neighbors with same shading as itself |
| W | Exactly 2 neighbors unshaded |
| X | In a singleton region |
| Y | Sees same distance up and down |
| Z | No unshaded 2x2 globally |
We can see that with these rules, it is impossible to make all the cells correct, e.g., in the first row, there is an H and a R, whose rules directly contradict each other. Instead, according to the flavor text, our aim is to make exactly one error in each row.
The completed grid is shown below (walkthrough below).

Taking the letters from the wrong cells, we get the first clue phrase HAMMING CODES.
Hamming codes is a family of error correcting codes of length 2r - 1. Read each row as a 15-bit string, treating unshaded/shaded as 0/1. Each row can be corrected to a valid Hamming code by flipping one bit. The correction bits are shown below.

This gives the second clue phrase NOW IN REVERSE. Now we take each row, reverse it and apply the Hamming code correction again (then reverse it back), e.g., in the first row, the reverse string is 001011101111010, where the underlined bit is where we should correct the bit. The correction bits are shown below.

This gives the third clue phrase PARITY MATRIX. This is referring to the parity-check matrix, a way to describe linear codes, for which the Hamming code is an example. More precisely, for a parity-check matrix H, the set of valid codewords are all x satisfying Hx = 0.
Treat the entire grid as a parity-check matrix, then correct each row into a valid codeword. This can be done by flipping exactly one bit in each row. The correction bits are shown below.

This gives the fourth clue phrase IV CELLS BELOW. Look at the cells 4 steps below these, where going past the bottom row loops back to the top. This spells the final answer ORLANDO BLOOM.

Remark: Treating unshaded/shaded as 1/0 instead of 0/1 does not change the solution at all. This is possible for Hamming codes because 111111111111111 is a valid code, and is possible for our parity matrix code because each row has an odd number of shaded cells, and 15 is odd.
Appendix
In the first row, H and R contradict each other. Hence, one of them is wrong, and all other letters in that row are correct. In particular, the Q is correct. In row 7, there are 2 Zs, which are both wrong or both correct. Hence, they are both correct. So globally, we must have no 2x2 shaded or unshaded areas.
- The P in r1c3 implies that the 4 cells r1c2, r2c2, r1c4, r2c4 are shaded.
- Thus r2c2 is wrong, and all others in row 2 are correct.
- The E's in rows 1 and 2 are shaded.
- The D in r1c13 implies that r2c12 and r2c14 are shaded.
- The V in r1c15 implies that r1c14, r1c15 and r2c15 are all unshaded.
- The S's imply that the region is completed.

- The J-piece in row 1 can only go sideways and shaded.
- The A and U in r2c5, r2c6 are unshaded. r2c7 is shaded.
- A cannot touch the border, so r1c5 and r1c6 are shaded.
- I in r1c2 cannot be in a 1x3, so r1c3 is unshaded and r3c2 is unshaded.
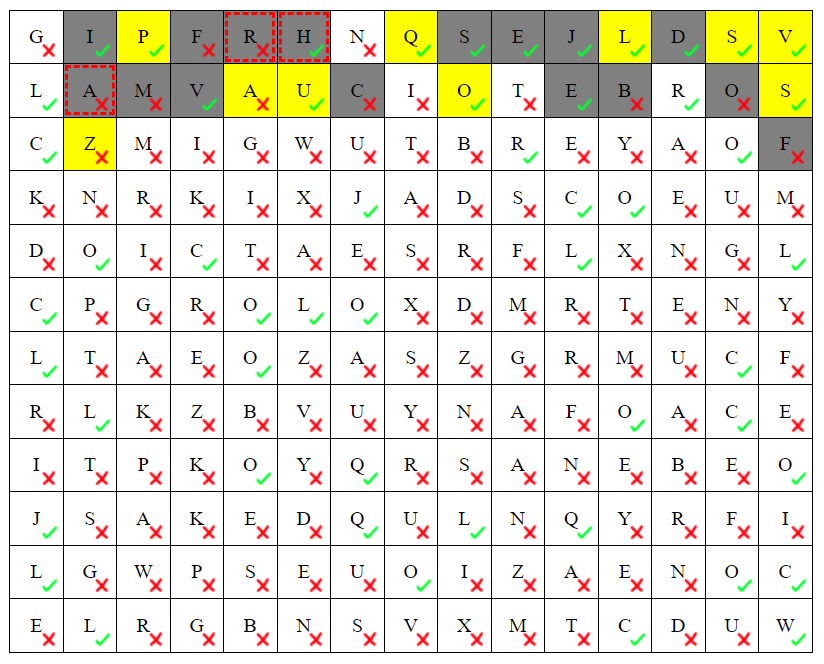
- If the M in r3c3 is right, it must be unshaded. But then r3c4 is wrong. So one of r3c3 and r3c4 is wrong.
- The C in r2c7 can only see the border upwards.
- One of r12c14 and r12c15 is right; either way gives r12c14 unshaded.

- We claim that one of r4c14 and r4c15 is wrong.
- If they were both right, r7c15 is wrong.
- But then, r7c14 is also wrong.

- Now one of r4c14 and r4c15 is wrong.

- Now r3c3 is wrong, and is shaded.
- The K, E, D in r10c4-6 cannot be all correct, so one of them is wrong.
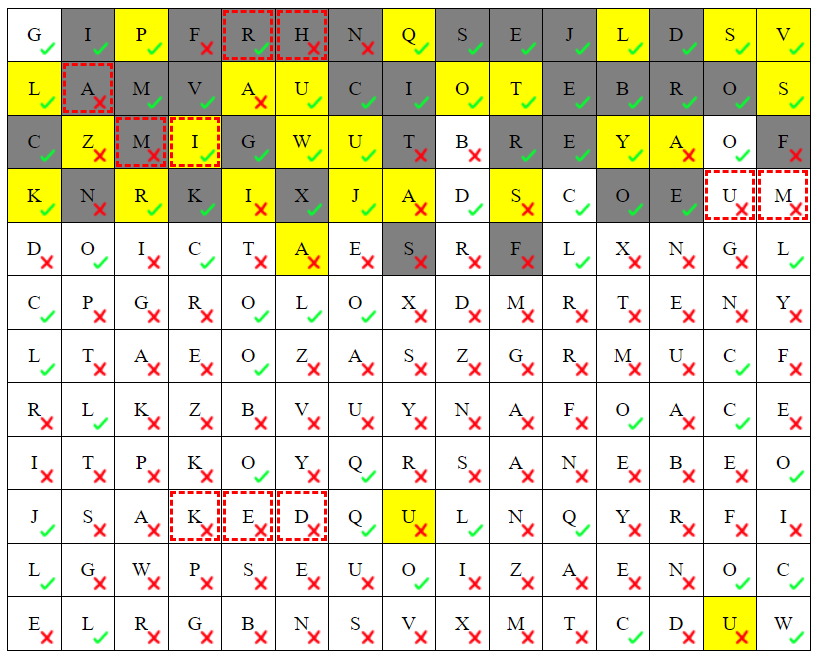
- We claim that one of r5c3, r5c4 is wrong.
- If they are both correct, the C must see the border downwards.
- Seeing through a shaded or unshaded region both lead to a contradiction.

- The N in r1c7 must find another N, so r3c9 is shaded.
- All F's must be correct and be in the same region. In particular, they are shaded.
- The C in r7c14 (if correct) can only see the border to the right.
- The U in r7c13 and C imply that r7c14 is shaded.
- If E in r6c13 is right, then the N in r6c14 is in an isolated region, so is wrong. So either r6c13 or r6c14 is wrong.

- The R in r3 implies r3c14 is shaded.
- r4c15 is wrong, so r4c14 is correct.
- The G is r7c10 is wrong: there is no way the giant shaded region is symmetric.
- r8c14 and r8c15 cannot both be correct.
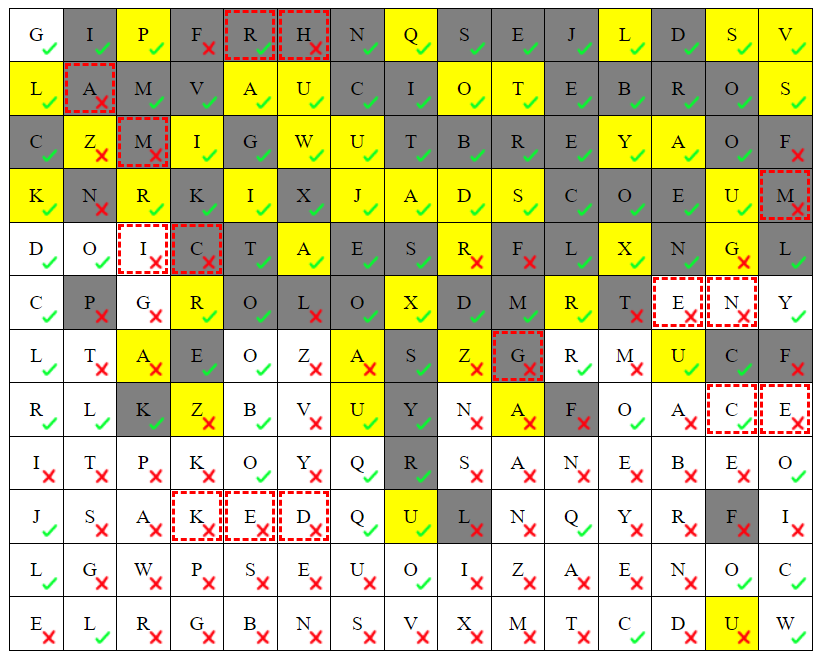
- The D in r10c6 is wrong:
- If it is correct, then r11c7 and r9c4 are wrong.
- The N in r4c2 cannot find another N.
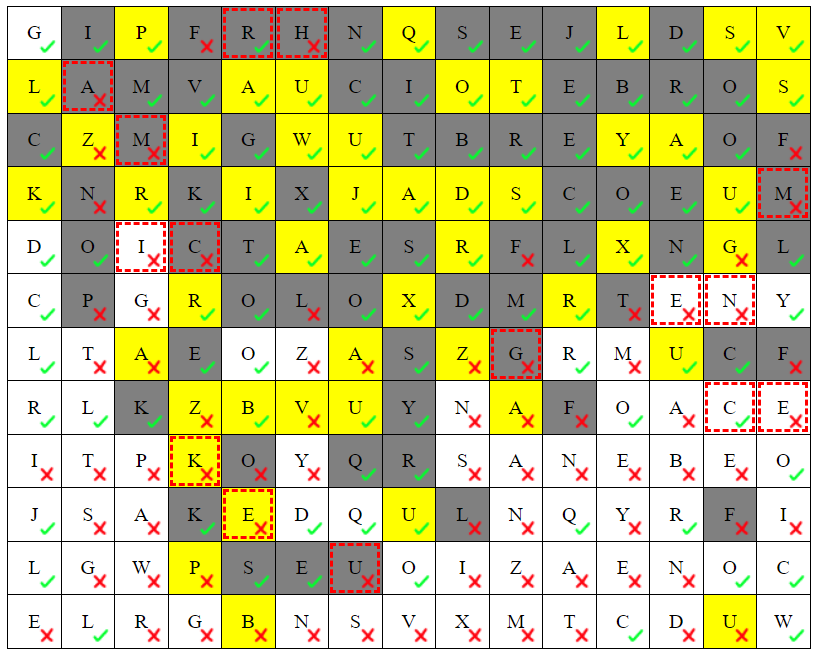
- r9c4 and r9c5 cannot both be correct.
- Otherwise, r8c5, r7c5 are shaded, r7c6 and r9c6 are unshaded, then r8c6 is wrong.
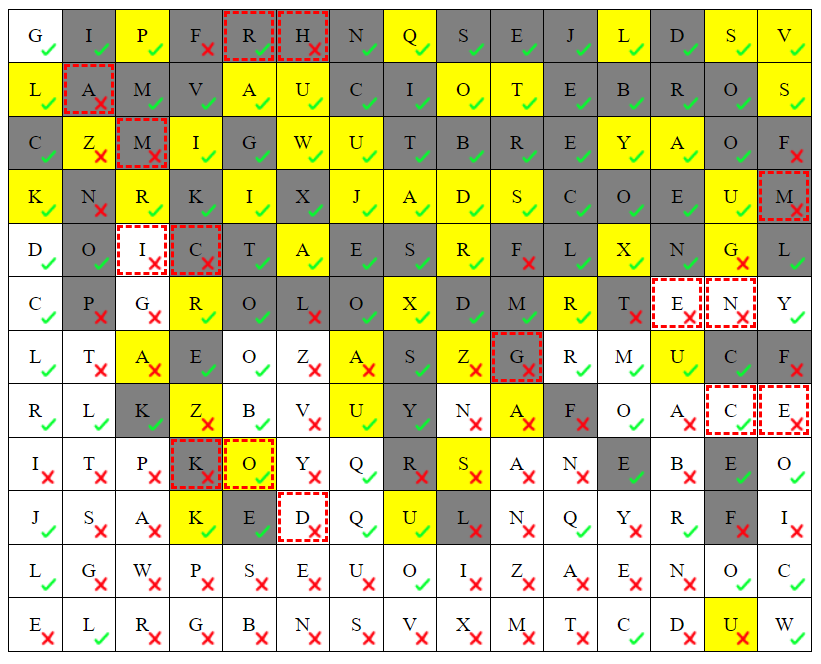
- The N in r8c9 is shaded, otherwise r9c10 is shaded then N's region is isolated with no other N's.
- The N's region must escape via r9c7.
- No new N's can connect to the F region, so r9c11 and r6c14 are unshaded.
- If the N in r6c14 is correct, it must find another N in a rotationally symmetric region, which is impossible.

- If the G in r6c3 is shaded, the N in r4c2 must be in a rotationally symmetric region, which is impossible.
- Now r5c3 is wrong.

- The N in r4c2 must still find another N, via the bottleneck at r9c6.
- Now r9c5 and r11c6 are wrong.

- By counting the parity of the number of N's, the N in r12c6 is correct.
- The only way for that N to find another N is via a shaded region through the S in r12c7. So r12c7 is wrong. We now have all the wrong cells.

- The X in row 12 is in an isolated region.

- The completed grid.
