Solve for Ewe
Word Clues
First, we look at the story and the clues. Each clue solves to a word that fits in a blank of the story. From the story, we can get an enumeration (a length in feet) for each word. For example, “gathered together” is the clue for “The rams ASSEMBLED (427.8213’) near the President's house.” The clues are given in alphabetical order by the word to make this easier.
| Clue | Word | Length |
|---|---|---|
| one who tries to bring about disorder due to absence of authority | ANARCHIST | 77.6870 |
| one who expresses creativity in a visual form | ARTIST | 23.0358 |
| gathered together | ASSEMBLED | 427.8213 |
| groups organized for a joint purpose | ASSOCIATIONS | 374.0699 |
| theft or misappropriation of funds | EMBEZZLEMENT | 425.6831 |
| symbolic representation | EMBLEM | 226.7377 |
| involved in complicated circumstances which are difficult to escape | ENTANGLED | 210.3977 |
| equal treatment of all disputants | IMPARTIALITY | 103.6350 |
| put a decision into effect | IMPLEMENT | 206.6847 |
| relative physical positions or directions | ORIENTATIONS | 331.3562 |
| begin to exist | ORIGINATE | 363.1130 |
| situation in which progress seems impossible | STALEMATE | 249.4009 |
| odorless, tasteless white substance found in potatoes | STARCH | 31.8332 |
| official account of facts | STATEMENT | 85.5501 |
| the property of having not previously been processed or woven | VIRGINITY | 147.0974 |
Trigram Placement
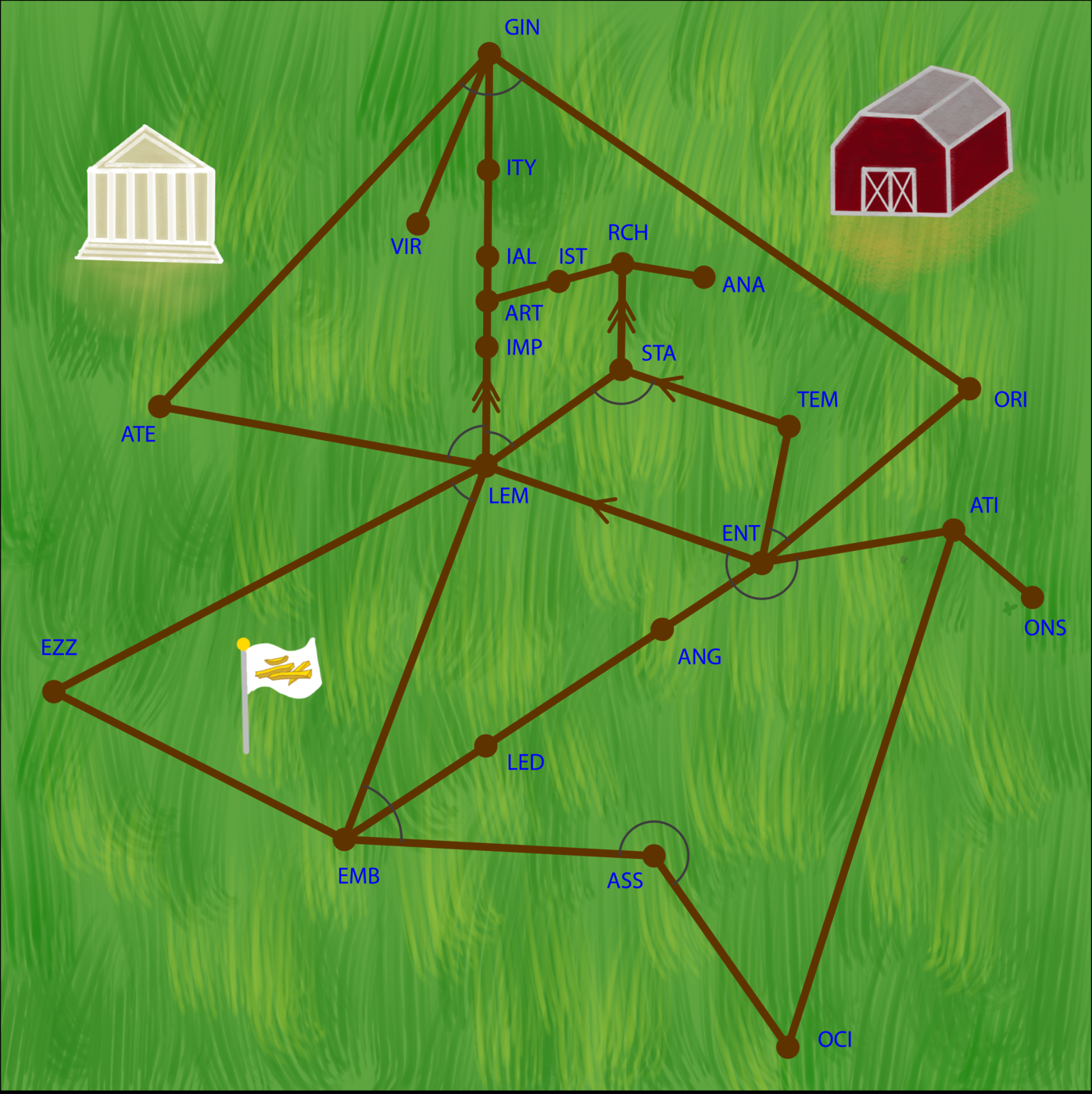
We notice that each word’s length is a multiple of 3. If we split the words into 3-letter sections, also known as trigrams, we can see there are many repeated trigrams. For example, ENT appears in EMB-EZZ-LEM-ENT, ORI-ENT-ATI-ONS, ENT-ANG-LED, etc. (This property could also help with solving all of the words.) One possible break in is to notice that the number of unique trigrams is the same as the number of nodes in the graph.
Also, we see that the enumerations are given in feet. The measurements of the fences in the image are also given in feet. This leads us to believe that words will map onto combinations of edges on the graph. One possible break-in is to notice that two given values on the graph, 112.3860’ and 98.0118’, sum to 210.3977’, which is the enumeration for ENTANGLED.
We place each trigram on the graph such that any word can be found as a path in the graph (i.e. stepping from node to node without backtracking or making a loop). Additionally, the edge lengths in the path sum to the enumeration for the word. Using these conditions, we can logically determine where all the trigrams go.
Trigonometry Solving
Next, we carefully solve for the missing dimensions of the diagram. Using the given dimensions and the enumerations for each word, we can solve the rest using basic trigonometry, law of sines and cosines, and geometric properties. One way to solve a polygon with more than 3 sides is to add construction lines that split it into triangles.
There are 8 angles which have rams in them, and the goal is to solve for these.
This table lists the dimensions.
| Vertex 1 | Vertex 2 | Length (ft) |
| ANA | RCH | 32.4230 |
| RCH | IST | 45.2640 |
| ART | IST | 23.0358 |
| ASS | EMB | 281.8676 |
| EMB | LED | 145.9537 |
| ASS | OCI | 90.2935 |
| OCI | ATI | 192.8471 |
| ATI | ONS | 90.9293 |
| EMB | EZZ | 106.7055 |
| EZZ | LEM | 142.7021 |
| LEM | ENT | 176.2755 |
| EMB | LEM | 226.7377 |
| ENT | ANG | 98.0118 |
| ANG | LED | 112.3860 |
| IMP | ART | 66.2086 |
| ART | IAL | 21.7634 |
| IAL | ITY | 15.6631 |
| IMP | LEM | 30.4092 |
| ORI | ENT | 100.9847 |
| ENT | ATI | 139.4422 |
| ORI | GIN | 111.5443 |
| GIN | ATE | 251.5686 |
| STA | LEM | 112.1621 |
| LEM | ATE | 137.2388 |
| STA | RCH | 31.8332 |
| STA | TEM | 38.2754 |
| TEM | ENT | 47.2747 |
| VIR | GIN | 113.7635 |
| GIN | ITY | 33.3339 |
This table lists the angles.
| Angle | Magnitude (deg) |
| LEM-ATE-GIN | 38.4109 |
| ATE-GIN-LEM | 30.6253 |
| GIN-LEM-ATE | 110.9638 |
| STA-LEM-ART | 33.5438 |
| LEM-ART-RCH | 114.8462 |
| ART-RCH-STA | 65.1538 |
| RCH-STA-LEM | 146.4562 |
| ENT-LEM-STA | 18.3099 |
| LEM-STA-TEM | 161.6901 |
| STA-TEM-ENT | 131.8105 |
| TEM-ENT-LEM | 48.1895 |
| RCH-ART-GIN | 65.1538 |
| ART-GIN-ORI | 109.2772 |
| GIN-ORI-ENT | 90.0000 |
| ORI-ENT-TEM | 60.6796 |
| EZZ-LEM-EMB | 21.0640 |
| LEM-EMB-EZZ | 28.7283 |
| EMB-EZZ-LEM | 130.2077 |
| EMB-LEM-ENT | 123.8301 |
| LEM-ENT-EMB | 31.9075 |
| ENT-EMB-LEM | 24.2624 |
| EMB-ENT-ATI | 156.7637 |
| ENT-ATI-OCI | 53.1296 |
| ATI-OCI-ASS | 90.0000 |
| OCI-ASS-EMB | 225.1293 |
| ASS-EMB-ENT | 14.9774 |
Extraction
Taking a closer look at the pictured rams, along with the flavortext that they love trigonometry, we see that there are 3 varieties of horns, shaped like the sine, cosine, and tangent functions. We count the number of each type of sheep for each angle, to get an equation a⋅sin(x) + b⋅cos(x) + c⋅tan(x), where a is the number of sin sheep, b is the number of cos sheep, etc. For example, ATE is 38.4109° and has 1 sin sheep and 3 tan sheep.
sin(38.4109°) + 3⋅tan(38.4109°) = 3.00000…
This is suspiciously close to a whole number. All of the angles similarly solve to a whole number. (This property could allow us to check our math work as we go.)
| Trigram | Angle (deg) | # sin | # cos | # tan | a⋅sin(x) + b⋅cos(x) + c⋅tan(x) | Letter |
|---|---|---|---|---|---|---|
| VIR | 0 | 2 | 1 | 1 | 1 | V |
| ATE | 38.4109 | 1 | 0 | 3 | 3 | E |
| ENT | 48.1895 | 0 | 3 | 0 | 2 | N |
| ATI | 53.1296 | 1 | 2 | 0 | 2 | T |
| RCH | 65.1538 | 0 | 2 | 1 | 3 | H |
| OCI | 90 | 1 | 2 | 0 | 1 | O |
| LEM | 123.8301 | 3 | 0 | 1 | 1 | L |
| EZZ | 130.2077 | 3 | 2 | 0 | 1 | E |
Once we’ve calculated all of these, we see that all the numbers are 1, 2, or 3, which leads us to believe they are indices for the trigram at the angle. Indexing into the trigram and sorting by the angle gives us the answer, VENTHOLE.