Once the pieces are cut out, assembling them into the labyrinth proceeds in two stages:
Squares assembled
The half-squares are assembled in pairs into squares, by assembling each mintotaur (figure with bull horns and human feet) so the "horns" clue answer is the "feet" clue answer with MOO or LOW added. The set of squares is then:
| Horns clue | Answer | Feet Clue | Answer | North | East | South | West |
|---|---|---|---|---|---|---|---|
| Bridge unit | SMOOT | Ave. crosser | ST. | 0001 | 1001 | 0110 | 1001 |
| Chandler tec | MARLOWE | She-horse | MARE | 1001 | 0110 | 0101 | 0010 |
| Debated | MOOTED | Keanu role | TED | 1101 | 1111 | 1111 | 1110 |
| Dinero | MOOLA | Sol follower | LA | 0110 | 0001 | 0110 | 1001 |
| Docking | MOORING | Annulus | RING | 0101 | 0001 | 1110 | 0010 |
| Emptily | HOLLOWLY | Ilex | HOLLY | 1001 | 0010 | 1000 | 1010 |
| Immature | CALLOW | Mr. Ripken | CAL | 0111 | 0010 | 0110 | 0111 |
| Lily or rose | FLOWER | Iron in Paris | FER | 0001 | 1111 | 1010 | 0010 |
| Luna | THE MOON | At that time | THEN | 1000 | 1000 | 1011 | 1011 |
| Sacred | HALLOWED | Dragged | HALED | 0111 | 0111 | 1000 | 1000 |
| Schnorrer | MOOCHER | Clueless role | CHER | 1110 | 0101 | 0001 | 0010 |
| Scram | VAMOOSE | Urn | VASE | 1010 | 1000 | 1000 | 1010 |
| Shindig | BLOWOUT | Fight | BOUT | 1111 | 1110 | 0101 | 1111 |
| Slender | WILLOWY | Sly | WILY | 0101 | 0010 | 1000 | 1111 |
| Damsel | 1110 | 0001 | 0010 | 0001 | |||
| Theseus | 1101 | 0101 | 1111 | 1111 | |||
Squares combined
The squares are then assembled into a 4x4 square, matched up by paths. The path patterns on the edge of the 1x1 squares are shown above (1 = path present, 0 = path absent, in clockwise order). We can deduce the assembly pattern as follows:
-
0010 matches with 0100, but no 1x1 has 0100 on any edge, so all 0010s must occur on the edge of the 4x4. Thus, the only 8 1x1s that can form part of the center 2x2 are (color coded for how they will be used in parts (2) and (3)):
Debated MOOTED Keanu role TED 1101 1111 1111 1110 Shindig BLOWOUT Fight BOUT 1111 1110 0101 1111 Theseus 1101 0101 1111 1111 Bridge unit SMOOT Ave. crosser ST. 0001 1001 0110 1001 Dinero MOOLA Sol follower LA 0110 0001 0110 1001 Luna THE MOON At that time THEN 1000 1000 1011 1011 Sacred HALLOWED Dragged HALED 0111 0111 1000 1000 Scram VAMOOSE Urn VASE 1010 1000 1000 1010 -
ST and LA only have one edge apiece (0001) that matches anything else in this set (the 1000 of THEN, HALED, and VASE), so if either one occurs in the central 2x2, they both have to, next to each other, touching two of THEN, HALED, and VASE at their 0001 edges; but then a 0110 of LA would be touching a 1001 of ST, which is impossible. Thus, ST and LA are not in the central 2x2.
-
Also, none of THEN, HALED, and VASE can touch each other, so if there is more than one of these in the central 2x2 there would have to be two, catercorner, touching two of TED, BOUT, and Theseus; however, TED cannot touch VASE, BOUT cannot touch THEN, and Theseus cannot touch HALED, so this is impossible. So there cannot be more than one of THEN, HALED, and VASE in the central 2x2, so that 2x2 must consist of one of these along with all of TED, BOUT, and Theseus. Of the six options for neighbors of THEN, HALED, and VASE only one allows the remaining one of TED, Theseus, and BOUT to be placed (orientations are given in parentheses):
VASE (v) 1010 0101 Theseus (v) VASE (v) 1010 0101 BOUT (>) 1010 1101 1010 1110 0101 0101 BOUT (v) 1111 X Theseus (<) 1111 X HALED (>) 0111 1110 BOUT (v) HALED (>) 0111 1110 TED (^) 0111 1111 0111 1111 1110 1110 TED (>) 1101 X BOUT (<) 0101 X THEN (<) 1011 1101 TED (<) THEN (<) 1011 1101 Theseus (<) 1011 1110 1011 1111 1101 1101 1111 Theseus (^) 0101 X TED (^) 1111 1111 BOUT (^) Up to rotation, we now have the following as the central 2x2, and need to fill in the edge 1x1s:
A B C D 1000 0101 L 1000 THEN (<) 1011 1101 Theseus (<) 1111 E 1011 1111 1101 1111 K 1110 TED (^) 1111 1111 BOUT (^) 1110 F 1111 0101 J I H G -
The two 1000s on THEN have to be matched by 0001s that are not adjacent to a 0010. Only ST, LA, and RING have such a 0001. The six possibilities are:
0110 0110 LA (>) 1001 1001 ST (v) 1010 0001 1010 0001 0101 1000 0101 1000 RING (^) 0001 1000 THEN (<) RING (^) 0001 1000 THEN (<) 0111 1110 RING (>) 0111 1110 RING (>) 0110 0001 1001 0001 0110 1000 1001 1000 LA (^) 0001 1000 THEN (<) ST (>) 0001 1000 THEN (<) 0110 0110 LA (>) 1001 1001 ST (v) 1001 0001 0110 0001 1001 1000 0110 1000 ST (>) 0001 1000 THEN (<) LA (^) 0001 1000 THEN (<) Of these, only the last allows any 1x1 to fit into A corner, and only MARE (>) fits there.
-
The B-C edge is now 1001-1001, and the L-K edge is now 0110-0110, so HOLLY (<) must be in C and CAL (v) must be in K. Also, E and I must contain the only two remaining 1x1s with a 1111 edge, FER and WILY. Putting FER (<) in I and WILY (^) in E leaves no possibilities for F and H. Putting FER (v) in E and WILY (>) in I forces F to be HALED (v) and H to be VASE (^). Up to rotation, we now have:
0010 0110 0010 0101 MARE (>) 1001 1001 ST (v) 1001 1001 HOLLY(<) 1000 D 0110 0001 1010 0110 1000 0101 1010 1001 LA (^) 0001 1000 THEN (<) 1011 1101 Theseus (<) 1111 1111 FER (v) 0010 0110 1011 1111 0001 0110 1101 1111 1000 0010 CAL (v) 0111 1110 TED (^) 1111 1111 BOUT (^) 1110 0111 HALED (v) 1000 0111 1111 0101 0111 1111 1010 J 1000 WILY (>) 0101 1010 VASE (^) 1000 G 0010 1000 -
Finally, CHER's 1110 and 0001 are not adjacent, so it cannot go in J or G and must go in D as CHER (>), RING's 1110 is clockwise from its 0001, so it cannot go in J and must go in G as RING (v), and finally by elimination the Damsel must go in J as Damsel (^). As per the instructions, the Damsel needs to be upright; here, since she already is upright, we do not need to rotate the 4x4 further. The final, assembled 4x4 is:
We can now trace a path from Theseus, through all the minotaurs, to the damsel and out of the labyrinth. This path crosses the Latin word VIR on leaving Theseus, and for everyone else crosses a cluster of one or two consonants on arriving and a vowel on leaving; putting these consonants and vowels together, in path order, we have the following:
| 1x1 square | Orientation | Text |
|---|---|---|
| Theseus | < | VIR |
| FER | v | MI |
| CHER | > | DA |
| HOLLY | < | TI |
| ST | v | PA |
| MARE | > | WE |
| LA | ^ | TO |
| CAL | v | NU |
| THEN | < | WA |
| BOUT | ^ | TA |
| RING | v | QE |
| HALED | v | PI |
| VASE | ^ | TWE |
| WILY | > | KA |
| TED | ^ | RU |
| Damsel | ^ | JO |
Each of the consonant(s)-vowel combinations is the conventional spelling of a syllable represented by a character in Linear B (a system for writing Greek, originating on Crete, that predates the Greek alphabet); VIR is the conventional name for the Linear B ideogram for "man." Taking these Linear B characters, in the same orientations as the figures, along the path, we have:
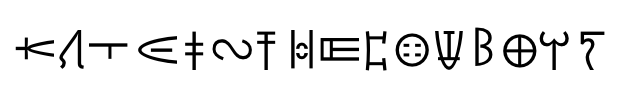
forming the clue KATE IN THE COWBOYS; the answer is the actress who played Kate in the 1972 film The Cowboys, COLLEEN DEWHURST.

