Solution to Yes or No?
Upon opening this puzzle, we are presented with a table containing a number of phrases, placed seemingly at random. Some of the clues are bolded, and the dashes on the right match the number of bolded clues in each row.
A little research allows us to determine the truth value of each clue, or, in at least one case, resolve the clue to the word TRUE. Treating the truth values of the bolded clues as binary, we can read each row as a letter by indexing the resulting binary number into the alphabet.
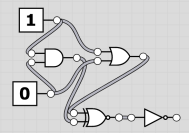 This logic circuit
outputs 1. This logic circuit
outputs 1. |
Gigabytes and gibibytes are the same size according to the International Electrotechnical Commission. | 10 | B | |||
| Quick-break technology, which the modern light switch is based on, was patented in 1884. | The Binary is an office building in Cairo, Egypt. | Ammonium chloride is a binary compound. | P ⊆ NP | 1001 | I | |
| The first version of what would become JavaScript was written in ten days. | Huffman coding is a method of creating an optimal prefix code. | Charles Babbage never completed a working version of his Analytical Engine. | It is possible to write both eight and negative eight in two's complement form using only four bits each. | 1110 | N | |
| Stuxnet was a cyberattack designed to damage equipment of the Iranian Nuclear Program. | 1 | A | ||||
| ENIAC was decommissioned a little less than 10 years after its first practical use. | The Python programming language is named after the snake. | Binary fission is a form of sexual reproduction. | Ada Lovelace published the first computer algorithm in Notes. | 1001 | I | |
| The Dog Star is actually a binary star system. | Boolean algebra was first introduced in Gödel, Escher, Bach, an Eternal Golden Braid. | The word 'byte' came about because of a misspelling in an internal missive. | AVL trees and red-black trees are both types of binary trees. | The binary search algorithm performs at least n2 operations in the worst case, where n is the number of elements in the array being searched. | 10010 | R |
| A false dichotomy is the reduction of a situation to two options, when other options exist. | C# was called "Cool" (C-like Object Oriented Language) prior to being named C#. | 01010100 01010010 01010101 01000101 | A provably secure hash function is an example of a one-way function. | 1111 | O | |
BINAIRO is a type of logic puzzle using solely 0s and 1s. The rules can be found here. Using the truth values of the bolded clues as givens, we can treat the grid as an 8×8 Binairo puzzle. The puzzle has a unique solution, given below. Please see the appendix for a step-by-step solution to the puzzle.
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
If we take 1 as true and 0 as false in the above solution, we can assign a true or false value to each of the non-bolded clues. This gives us the information below.
| Statement | Truth Value |
|---|---|
| The first letter of the answer is in the word PUZZLE. | F |
| The last letter of the answer appears in the title. | T |
| The third letter of the answer is a consonant. | F |
| The answer has fewer letters than the title. | T |
| The first letter of the answer has exactly one enclosed space when written as a capital letter. | T |
| The first three letters of the answer form a valid English word. | T |
| The penultimate letter of the answer is in the word BOXLIKE. | F |
| The length of the answer is divisible by two. | F |
| The answer is playable in a game of English Scrabble. | T |
| The last letter of the answer is one of the 18 least frequent letters in the English language. | F |
| The length of the answer is divisible by three. | F |
| The penultimate letter of the answer is a consonant. | T |
| The last letter of the answer is not in the word TRUE. | T |
| The second letter of the answer has an enclosed space when written as a capital letter. | F |
| The third letter of the answer is in the first six letters of the English alphabet. | T |
| The last letter of the answer has exactly one enclosed space when written as a capital letter. | F |
| The number of vowels in the answer is even. | T |
| The last letter of the answer has exactly one enclosed space when written as a capital letter. | F |
| The second letter of the answer has a curved stroke when written as a capital letter. | T |
| The penultimate letter of the answer is usually written without lifting the pencil in lower case. | F |
| The first letter of the answer is not adjacent to a vowel in the alphabet. | F |
Using this information, we can deduce the answer to the puzzle as follows.
- The answer is playable in a game of English Scrabble. This excludes any proper nouns.
- The length of the answer is not divisible by two or three, and the answer has fewer letters than the title does. The length must be five.
- The first letter of the answer is adjacent to a vowel in the alphabet, has exactly one enclosed space when written as a capital letter, and is not in the word PUZZLE. The first letter must be D.
- The last letter of the answer is one of the eight most frequent letters of the English alphabet, has no enclosed spaces when written as a capital letter and is not in the word TRUE. It, however, is in the title of the puzzle. The last letter must be either N or S.
- The fourth, or penultimate, letter of the answer is not normally drawn with a single stroke in lowercase, is a consonant, and is not in the word BOXLIKE. The fourth letter must be one of D, F, P, or T.
- The number of vowels in the answer is even. Because the length is five, and three of the letters are consonants, there must be two vowels. Specifically, the second and third letters are vowels.
- The second letter is a vowel, has no enclosed spaces, and has a curved stroke when written as a capital letter. The second letter must be U.
- The third letter is a vowel and within the first six letters of the English alphabet. The third letter must be either A or E, but since the first three letters must form a valid English word and DUA isn’t a word, the third letter must be E.
This gives us an answer of DUE[DFPT][NS], which must be DUETS, an appropriate answer to this puzzle of duality.
The initial BINAIRO puzzle looks like this after resolving the clues.
| 1 | 0 | ||||||
| 1 | 0 | 0 | 1 | ||||
| 1 | 1 | 1 | 0 | ||||
| 1 | |||||||
| 1 | 0 | 0 | 1 | ||||
| 1 | 0 | 0 | 1 | 0 | |||
| 1 | 1 | 1 | 1 | ||||
Applying the first two rules repeatedly allows us to reach the following state:
| 0 | 1 | 0 | |||||
| 1 | 0 | 0 | 1 | 0 | 1 | ||
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | ||
| 1 | 0 | 1 | 0 | 0 | 1 | ||
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 |
At this point, we can fill in the bottom row. We note that if the bottom right corner were a 1, the rightmost column would have three 0s in a row, which is not allowed. Therefore, the bottom right corner is a 0.
Similarly, the last 0 in the bottom row must go in the third column. If it were in any other column, there would be three 1s in a row in the bottom row.
The grid now looks like this:
| 0 | 1 | 0 | |||||
| 1 | 0 | 0 | 1 | 0 | 1 | ||
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | ||
| 1 | 0 | 1 | 0 | 0 | 1 | ||
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
Now we look at duplicate columns. The fourth column is identical to the sixth column, except for its two blank cells. Therefore, we must fill the cells in the fourth column with the opposite values of those in the sixth column.
The same is true of the eighth and fifth columns. The grid now looks like this:
| 1 | 0 | 0 | 1 | 0 | 1 | ||
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | ||
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
Finally, we apply the first two rules a few more times to finish the puzzle.
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |