Solution to Ignorance
This puzzle contains many logic puzzles similar in spirit to the famous Cheryl’s Birthday problem. Each logic puzzle starts with Cheryl (in one case, Denise) giving Albert and Bernard partial information about some piece of data (e.g., her birthday, a set of numbers, a nonogram, etc.). Albert and Bernard then have a conversation about what they know and don’t know about the data. Based on this conversation, we can recover the original information given to Albert and Bernard by Cheryl, and more importantly, we can recover the values of the various italicized variables.
At the end of the puzzle, Cheryl tells Albert the first half of the answer to this puzzle and Bernard the second half of the answer to this puzzle. Albert and Bernard then have one final conversation about the answer to this puzzle, but where bits and pieces of their conversation are replaced with variables referencing earlier subpuzzles; for example, in Albert’s first line, Albert states “I don’t know if the answer contains exactly product vowels”. By solving the 8th subpuzzle, we can find that the value of product is 4, so Albert (at the beginning of the conversation) does not know if the answer contains exactly 4 vowels. Solving this final puzzle gives us the answer to the puzzle, BRUTES.
Below we provide full solutions to each of the subpuzzles and the final “meta” subpuzzle. Before we begin, some general tips that are useful across several of the subpuzzles:
- It’s often useful to note that, at any point in any conversation, any deduction that you the solver can make is also something that all conversing parties can make, and furthermore that all conversing parties know that other parties can make and so on (that is, it’s common knowledge.)
- In many of the subpuzzles, it is possible to represent the state of all knowledge (Albert’s knowledge, Bernard’s knowledge, and our knowledge) succinctly in a large table, where the rows correspond to Albert’s partial information and the columns correspond to Bernard’s partial information. In this table, we keep track of a subset of cells which could possibly correspond to the original piece of data. For example, in the original Cheryl’s birthday puzzle (and the first subpuzzle), we keep track of the possible dates of Cheryl’s birthday in a table where each row corresponds to a month (what Albert is told) and each column corresponds to day (what Bernard is told).
In this framing, whenever Albert makes a statement he reveals some information about the row of the table containing the answer, and this allows us to eliminate some rows. Similarly, whenever Bernard makes a statement, we can eliminate some columns. - One common statement is when Albert (for example) says “I don’t know if X is true”. In this case there has to be some choice of Bernard’s column which causes X to be true, and some choice of column which causes X to be false, and we can eliminate all rows for which X is either always true or always false.
- Alternately, you might prefer to think about representing each problem as a bipartite graph, where the vertices on one side correspond to possibilities for what Albert is told, vertices on the other side correspond to possibilities for what Bernard is told, and there is an edge between two vertices v and w if it is simultaneously possible that Albert was told v and that Bernard was told w.
Statements now allow us to remove vertices (and their incident edges) from the graph. For example, if Albert says “I don’t know Bernard’s piece of information”, this allows us to remove all of Albert’s vertices with degree 1.
Solutions to individual subpuzzles
birthmonth and birthday
This puzzle is actually isomorphic to the classic Cheryl’s birthday problem (i.e. it can be obtained from the classic Cheryl’s birthday problem by relabeling and reordering the months and the dates).
We can solve this puzzle as follows. Recall that the starting set of possible dates is given by the following table:
| May | 9 | 10 | ||||
|---|---|---|---|---|---|---|
| June | 8 | 11 | 12 | |||
| July | 11 | 12 | 13 | |||
| August | 8 | 10 |
Albert: I don't know when Cheryl's birthday is, but I know that Bernard doesn't know too.
No matter which month Cheryl’s birthday lies in, there is no way for Albert to know when Cheryl’s birthday is, so the first part of this statement gives us no information.
However, the second part of Albert’s statement (that he knows that Bernard does not know when Cheryl’s birthday is) does provide us with some information. If Bernard does not know when Cheryl’s birthday is, it must lie on a day that can possibly match with at least two different months. This immediately rules out the 9th and the 13th (which correspond uniquely to May and July respectively). Moreover, since Albert knows that Bernard doesn’t know when Cheryl’s birthday is, Cheryl’s birthday cannot belong to May or July.
We can therefore eliminate May 9, May 10, July 11, July 12, and July 13 as possible birthdays:
| May | 9 | 10 | ||||
|---|---|---|---|---|---|---|
| June | 8 | 11 | 12 | |||
| July | 11 | 12 | 13 | |||
| August | 8 | 10 |
Bernard: At first I didn't know when Cheryl's birthday is, but I know now.
Since Bernard now knows when Cheryl’s birthday is, it must now lie on a day which matches uniquely to a month. The only such days are the 10th, the 11th, and the 12th (which match with August, June, and June respectively). We can therefore eliminate June 8 and August 8:
| May | 9 | 10 | ||||
|---|---|---|---|---|---|---|
| June | 8 | 11 | 12 | |||
| July | 11 | 12 | 13 | |||
| August | 8 | 10 |
Albert: Then I also know when Cheryl's birthday is.
Since Albert knows when Cheryl’s birthday is, Albert’s month must contain only one possible date. Since June contains two possible dates (June 11 and June 12), Albert’s month must be August, and Cheryl’s birthday is August 10.
Answer: birthmonth = 8, birthday = 10
cell
For reference, here is the 10-by-10 table Cheryl starts with:
| 30 | . | . | . | . | . | . | . | . | . |
| . | . | 40 | 4 | . | 33 | 22 | . | . | 16 |
| 35 | . | 3 | . | . | . | 32 | . | . | . |
| 17 | . | . | . | . | . | . | . | . | 18 |
| . | . | . | . | . | . | 11 | . | . | . |
| . | . | 14 | . | 31 | . | . | . | . | |
| . | 21 | . | . | . | . | . | . | 13 | . |
| . | . | . | . | 15 | . | . | . | . | . |
| . | . | . | . | . | 12 | . | 20 | 34 | . |
| . | . | 26 | . | 9 | . | . | . | . | 23 |
Albert: I don't know the location of the cell.
If Albert does not know the location of the cell, his row must contain at least two numbered squares. We can thus eliminate the first, fifth and eighth rows above (which only contain one numbered square) and obtain the following table:
| . | . | 40 | 4 | . | 33 | 22 | . | . | 16 |
| 35 | . | 3 | . | . | . | 32 | . | . | . |
| 17 | . | . | . | . | . | . | . | . | 18 |
| . | . | 14 | . | 31 | . | . | . | . | |
| . | 21 | . | . | . | . | . | . | 13 | . |
| . | . | . | . | . | 12 | . | 20 | 34 | . |
| . | . | 26 | . | 9 | . | . | . | . | 23 |
Bernard: I don't know the location of the cell.
Similarly, we can eliminate columns with a unique numbered square. This allows us to eliminate columns 2, 4 and 8 above.
| . | 40 | . | 33 | 22 | . | 16 |
| 35 | 3 | . | . | 32 | . | . |
| 17 | . | . | . | . | . | 18 |
| . | 14 | 31 | . | . | . | |
| . | . | . | . | . | 13 | . |
| . | . | . | 12 | . | 34 | . |
| . | 26 | 9 | . | . | . | 23 |
Albert: I don't know the location of the cell.
We again eliminate rows with a unique numbered square.
| . | 40 | . | 33 | 22 | . | 16 |
| 35 | 3 | . | . | 32 | . | . |
| 17 | . | . | . | . | . | 18 |
| . | 14 | 31 | . | . | . | |
| . | . | . | 12 | . | 34 | . |
| . | 26 | 9 | . | . | . | 23 |
Bernard: I don't know the location of the cell.
We again eliminate columns with a unique numbered square.
| . | 40 | . | 33 | 22 | 16 |
| 35 | 3 | . | . | 32 | . |
| 17 | . | . | . | . | 18 |
| . | 14 | 31 | . | . | |
| . | . | . | 12 | . | . |
| . | 26 | 9 | . | . | 23 |
Albert: We could continue this conversation indefinitely (by repeatedly saying "I don't know the location of the cell") without either of us learning the location of the cell.
We finally arrive at the core of this subpuzzle. To begin, let us understand what happens to this table if Albert and Bernard do continue this conversation indefinitely. If we do this, then we continue eliminating rows and columns from the table until we are left with a “stable” table, where the statement “I don’t know the location of the cell” conveys no additional information (regardless of who says it). If we carry out this procedure, we end up eliminating the rows and columns highlighted below in red before arriving at this stable state.
| . | 40 | . | 33 | 22 | 16 |
| 35 | 3 | . | 32 | . | |
| 17 | . | . | . | 18 | |
| . | 14 | 31 | . | . | |
| 12 | |||||
| . | 26 | 9 | . | 23 |
Note that the cells deleted in this process (the cells highlighted in red) are exactly the cells where Albert and Bernard would learn the location of the cell during this conversation (instead of eliminating the cell, at that point in the conversation one of Albert or Bernard would have to say that they do in fact know the location of the cell).
Now, how can Albert know for a fact that he and Bernard can continue the conversation indefinitely? Albert must know that the true cell is not deleted in this process. Since the cells deleted in this process belong to the first and fifth rows, we can delete these rows from the table.
| 35 | 3 | . | 32 | . |
| 17 | . | . | . | 18 |
| . | 14 | 31 | . | . |
| . | 26 | 9 | . | 23 |
Bernard: I know the location of the cell.
Bernard now knows the location of the cell. That must mean that Bernard’s column contains a unique numbered cell. The only such column is the fourth column in the above table, which contains the cell numbered 32.
Answer: cell = 32
d1, d2, and d3
Since there are 6 possibilities for each of d1, d2, and d3, there are 216 possibilities for the numbers given to Albert, Bernard and Cheryl. While it’s possible to solve this puzzle by keeping track of all 216 possibilities in a 6-by-6-by-6 table, we will take a different approach (which will greatly reduce the set of possibilities we need to consider).
Let A, B, and C equal d2 + d3, d1 + d3, and d1 + d2 respectively.
Cheryl: I don't know if there are exactly two 1s among Denise's three numbers.
Note that if Cheryl’s number is larger than 7, it is impossible for either d1 or d2 to be equal to 1, so it is impossible for two of Denise’s three numbers to equal 1. We therefore know that C is less than or equal to 7. (It is also easy to check that any number between 2 and 7 is possible for C, but we will not need this).
Bernard: I don't know if there are exactly zero 1s among Denise's three numbers.
Note that if Bernard’s number B was 2 or 3, then that would guarantee at least one 1 among the numbers d1 and d3. It follows that B cannot be 2 or 3.
Interestingly, B cannot be 12 either. Note that if Bernard’s number is 12, d1 and d3 must both be 6. Then, if d2 > 1, we would have that C = d1 + d2 > 7, contradicting what we know from Cheryl’s first statement.
Any other value for B is possible. If 4 ≤ B ≤ 8, then (d1 , d2 , d3) = (3, 1, B−3) is one possible assignment where there is at least one 1, and (d1 , d2 , d3) = (2, 2, B−2) is a possible assignment where there are no 1’s. Similarly, if 9 ≤ B ≤ 11, (d1 , d2 , d3) = (5, 1, B−5) is one possible assignment where there is at least one 1, and (d1 , d2 , d3) = (5, 2, B−5) is a possible assignment where there are no 1’s.
Cheryl: I don't know if there are exactly two 6s among Denise's three numbers.
Similarly as in the first step, this implies that C ≥ 7 (since if C < 7, neither d1 nor d2 can be 6).
But now we know both that C ≤ 7 and C ≥ 7, so we must have that C = 7. It follows that d2 = 7 − d1, so we can parametrize the triple (d1, d2, d3) via just the value of d1 and d3. We do so in the following table, where the row corresponds to the value of d1 and the column corresponds to the value of d3.
| (1, 6, 1) | (2, 5, 1) | (3, 4, 1) | (4, 3, 1) | (5, 2, 1) | (6, 1, 1) |
| (1, 6, 2) | (2, 5, 2) | (3, 4, 2) | (4, 3, 2) | (5, 2, 2) | (6, 1, 2) |
| (1, 6, 3) | (2, 5, 3) | (3, 4, 3) | (4, 3, 3) | (5, 2, 3) | (6, 1, 3) |
| (1, 6, 4) | (2, 5, 4) | (3, 4, 4) | (4, 3, 4) | (5, 2, 4) | (6, 1, 4) |
| (1, 6, 5) | (2, 5, 5) | (3, 4, 5) | (4, 3, 5) | (5, 2, 5) | (6, 1, 5) |
| (1, 6, 6) | (2, 5, 6) | (3, 4, 6) | (4, 3, 6) | (5, 2, 6) | (6, 1, 6) |
We have highlighted in red the cells where B = 2, 3, or 12 (and are thus invalid). One nice feature of this table is that along the diagonals running from south-west to north-east, Bernard’s value is fixed, and along the anti-diagonals running from north-west to south-east, Albert’s value is fixed.
Albert: I don't know if there are exactly zero 6s among Denise's three numbers.
It suffices to check which anti-diagonals both contain a valid cell with zero 6s and a valid cell with at least one 6 — we can eliminate all other anti-diagonals in the above table. In particular, we can eliminate the anti-diagonals with A = 2, 7, 11, and 12.
| (1, 6, 1) | (2, 5, 1) | (3, 4, 1) | (4, 3, 1) | (5, 2, 1) | (6, 1, 1) |
| (1, 6, 2) | (2, 5, 2) | (3, 4, 2) | (4, 3, 2) | (5, 2, 2) | (6, 1, 2) |
| (1, 6, 3) | (2, 5, 3) | (3, 4, 3) | (4, 3, 3) | (5, 2, 3) | (6, 1, 3) |
| (1, 6, 4) | (2, 5, 4) | (3, 4, 4) | (4, 3, 4) | (5, 2, 4) | (6, 1, 4) |
| (1, 6, 5) | (2, 5, 5) | (3, 4, 5) | (4, 3, 5) | (5, 2, 5) | (6, 1, 5) |
| (1, 6, 6) | (2, 5, 6) | (3, 4, 6) | (4, 3, 6) | (5, 2, 6) | (6, 1, 6) |
Bernard: I don't know if there is exactly one 1 among Denise's three numbers.
Similarly, we check which diagonals both contain a valid cell with exactly one 1, and a valid cell with zero or two 1s. This allows us to eliminate the cells with B = 4 and 7.
| (1, 6, 1) | (2, 5, 1) | (3, 4, 1) | (4, 3, 1) | (5, 2, 1) | (6, 1, 1) |
| (1, 6, 2) | (2, 5, 2) | (3, 4, 2) | (4, 3, 2) | (5, 2, 2) | (6, 1, 2) |
| (1, 6, 3) | (2, 5, 3) | (3, 4, 3) | (4, 3, 3) | (5, 2, 3) | (6, 1, 3) |
| (1, 6, 4) | (2, 5, 4) | (3, 4, 4) | (4, 3, 4) | (5, 2, 4) | (6, 1, 4) |
| (1, 6, 5) | (2, 5, 5) | (3, 4, 5) | (4, 3, 5) | (5, 2, 5) | (6, 1, 5) |
| (1, 6, 6) | (2, 5, 6) | (3, 4, 6) | (4, 3, 6) | (5, 2, 6) | (6, 1, 6) |
Albert: I don't know if there is exactly one 6 among Denise's three numbers.
Again, we check for anti-diagonals which contain a valid cell with exactly one 6, and a valid cell with zero or two 6s. This allows us to eliminate the cells with A = 10.
| (1, 6, 1) | (2, 5, 1) | (3, 4, 1) | (4, 3, 1) | (5, 2, 1) | (6, 1, 1) |
| (1, 6, 2) | (2, 5, 2) | (3, 4, 2) | (4, 3, 2) | (5, 2, 2) | (6, 1, 2) |
| (1, 6, 3) | (2, 5, 3) | (3, 4, 3) | (4, 3, 3) | (5, 2, 3) | (6, 1, 3) |
| (1, 6, 4) | (2, 5, 4) | (3, 4, 4) | (4, 3, 4) | (5, 2, 4) | (6, 1, 4) |
| (1, 6, 5) | (2, 5, 5) | (3, 4, 5) | (4, 3, 5) | (5, 2, 5) | (6, 1, 5) |
| (1, 6, 6) | (2, 5, 6) | (3, 4, 6) | (4, 3, 6) | (5, 2, 6) | (6, 1, 6) |
Bernard: The number I was given is even.
We can eliminate all diagonals with an odd sum. In particular, we eliminate the remaining cells with B = 5, 9, and 11.
| (1, 6, 1) | (2, 5, 1) | (3, 4, 1) | (4, 3, 1) | (5, 2, 1) | (6, 1, 1) |
| (1, 6, 2) | (2, 5, 2) | (3, 4, 2) | (4, 3, 2) | (5, 2, 2) | (6, 1, 2) |
| (1, 6, 3) | (2, 5, 3) | (3, 4, 3) | (4, 3, 3) | (5, 2, 3) | (6, 1, 3) |
| (1, 6, 4) | (2, 5, 4) | (3, 4, 4) | (4, 3, 4) | (5, 2, 4) | (6, 1, 4) |
| (1, 6, 5) | (2, 5, 5) | (3, 4, 5) | (4, 3, 5) | (5, 2, 5) | (6, 1, 5) |
| (1, 6, 6) | (2, 5, 6) | (3, 4, 6) | (4, 3, 6) | (5, 2, 6) | (6, 1, 6) |
Albert: The number I was given is prime.
We can eliminate all non-prime anti-diagonals. In particular, we eliminate the remaining cells with A = 9.
| (1, 6, 1) | (2, 5, 1) | (3, 4, 1) | (4, 3, 1) | (5, 2, 1) | (6, 1, 1) |
| (1, 6, 2) | (2, 5, 2) | (3, 4, 2) | (4, 3, 2) | (5, 2, 2) | (6, 1, 2) |
| (1, 6, 3) | (2, 5, 3) | (3, 4, 3) | (4, 3, 3) | (5, 2, 3) | (6, 1, 3) |
| (1, 6, 4) | (2, 5, 4) | (3, 4, 4) | (4, 3, 4) | (5, 2, 4) | (6, 1, 4) |
| (1, 6, 5) | (2, 5, 5) | (3, 4, 5) | (4, 3, 5) | (5, 2, 5) | (6, 1, 5) |
| (1, 6, 6) | (2, 5, 6) | (3, 4, 6) | (4, 3, 6) | (5, 2, 6) | (6, 1, 6) |
Bernard: I now know Denise's three numbers.
In order for Bernard to know Denise’s three numbers, there must be a unique cell on the diagonal corresponding to Bernard’s number. There is only one choice of diagonal with a unique cell, and that is the diagonal with B = 10. It follows that (d1, d2, d3) = (6, 1, 4), the label of this unique cell.
Answer: d1 = 6, d2 = 1, d3 = 4.
div1 and div2
The possibilities for Albert’s number (div1) and Bernard’s number (div2) can be summarized in the following table of (div1, div2) pairs:
| (1, 2) | (1, 3) | (1, 4) | (1, 5) | (1, 6) | (1, 7) | |
| (2, 4) | (2, 6) | |||||
| (3, 6) | ||||||
Albert: Bernard doesn't know my number.
If div2 is prime, then Bernard knows that Albert’s number must be 1. On the other hand, if div2 is composite, then Bernard does not know Albert’s number (for example, it can be either 1 or the smallest prime divisor of Bernard’s number). Therefore, if Bernard doesn’t know Albert’s number, div2 is composite.
If Albert knows that Bernard doesn’t know Albert’s number, then Albert must know that Bernard’s number is composite. For the numbers in this table, this is possible if and only if div1 = 2 or 3; we can thus eliminate all cells with div1 = 1:
| (1, 2) | (1, 3) | (1, 4) | (1, 5) | (1, 6) | (1, 7) | |
| (2, 4) | (2, 6) | |||||
| (3, 6) | ||||||
Albert: Bernard still doesn't know my number.
Again, from the above table, we can see that Bernard does not know Albert’s number only if div2 = 6. In order for Albert to be sure that Bernard does not know Albert’s number, Albert must know that div2 = 6; this is only possible if div1 = 3. It follows that (div1, div2) = (3, 6).
Answer: div1 = 3, div2 = 6.
edges
The first thing to understand in this puzzle is that there are edges which are impossible to uniquely specify given only the connectivity data of the graph, but no other distinguishing features. For example, the two edges labelled 7 in the below graph are indistinguishable:
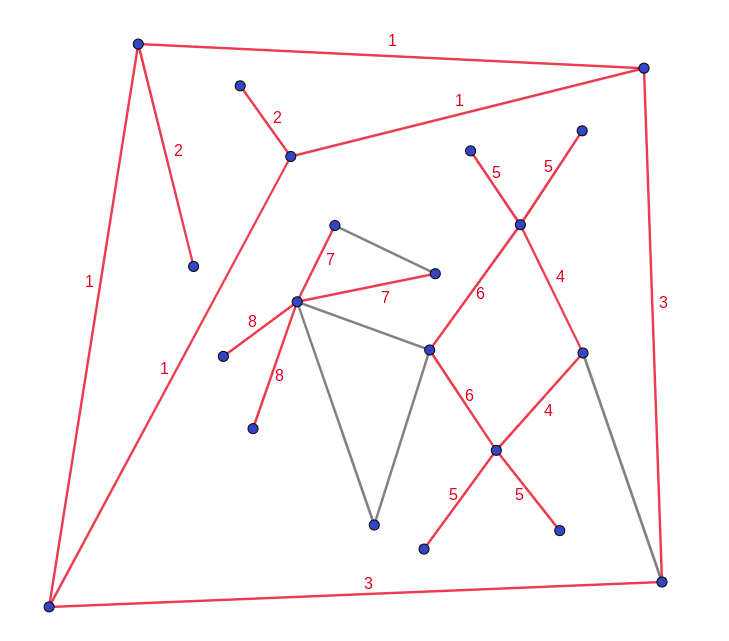
In particular, any true statement one can make about one of the edges labelled 7 that only uses the connectivity information of the graph will also be a true statement about the other edge labelled 7 — for example “this edge is adjacent to one vertex of degree 2 and one vertex of degree 6” is true for both edges. Mathematically, two edges are indistinguishable if there exists a graph automorphism mapping one edge to the other. In the above drawing, we have highlighted all indistinguishable edges in red, and labelled edges which are indistinguishable from each other with the same number.
In the analysis that follows, let us write E to denote Cheryl’s edge, A to denote the vertex given to Albert, and B to denote the vertex given to Bernard.
Albert: I don’t know if there’s any conversation we can have where I will learn which edge is Cheryl’s edge.
When is it the case that Albert cannot figure out which edge is Cheryl’s edge E? If Eis distinguishable from all other edges, then Albert and Bernard can both figure out which edge this corresponds to in their drawing by combining their information. If E is indistinguishable from some other edge, then it might still be the case that Albert can still identify E — for example, if only one of those two edges are incident with A. However, if Cheryl’s edge is indistinguishable from another edge incident with A, nothing Bernard can tell Albert can help Albert distinguish between the two edges (and identify E).
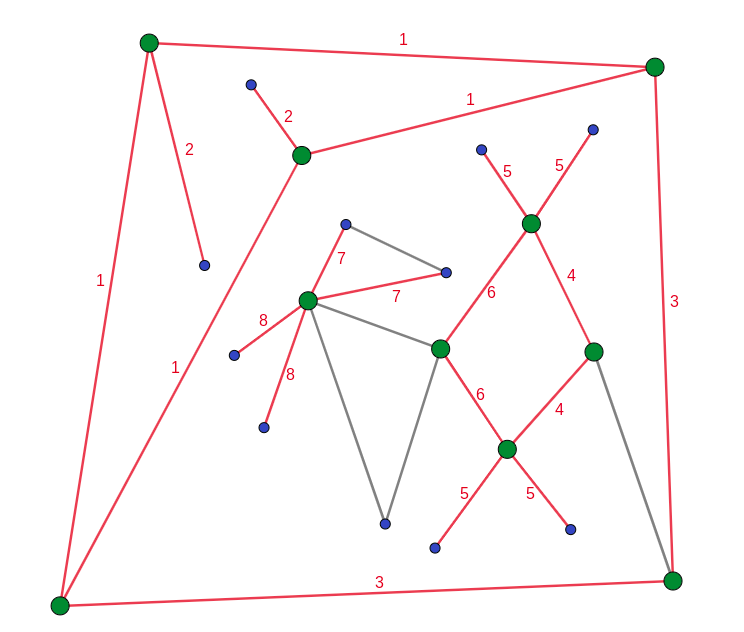
In summary, Albert cannot identify E iff A belongs to two red edges with the same label, one of which is E. Since Albert does not know if it is possible for him to identify E, A must be adjacent to at least two red edges with the same label, and to at least one other edge that is “distinguishable” for Albert (either a black edge or a red edge with a unique label among the red edges incident with A). This allows us to reduce the set of possibilities for A to the green vertices in the following image:
Bernard: I don’t know if there’s any conversation we can have where I will learn which edge is Cheryl’s edge.
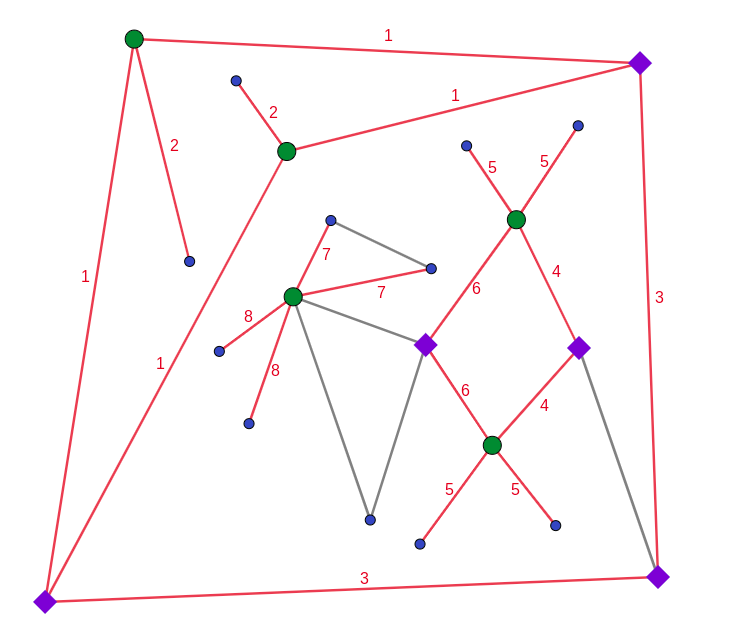
Similarly, Bernard does not know if it is possible for him to identify E. Similar to before B must be adjacent to two red edges with the same label and at least one other “distinguishable” edge — however now it is additionally important that these edges are not eliminated by what Bernard knows about the possibilities for A from Albert’s first statement (i.e. the other endpoints of these edges must be green vertices). From this, we can see that the only candidates for B are the purple diamonds in the following image:
Albert: I know Cheryl’s edge.
Since each purple diamond is a possible candidate for B, in order for Albert to know Cheryl’s edge (and thus B), A must be adjacent to a unique purple diamond. Since A must be either a green circle or purple diamond, this reduces the set of possibilities for A to the black crosses in the following image:
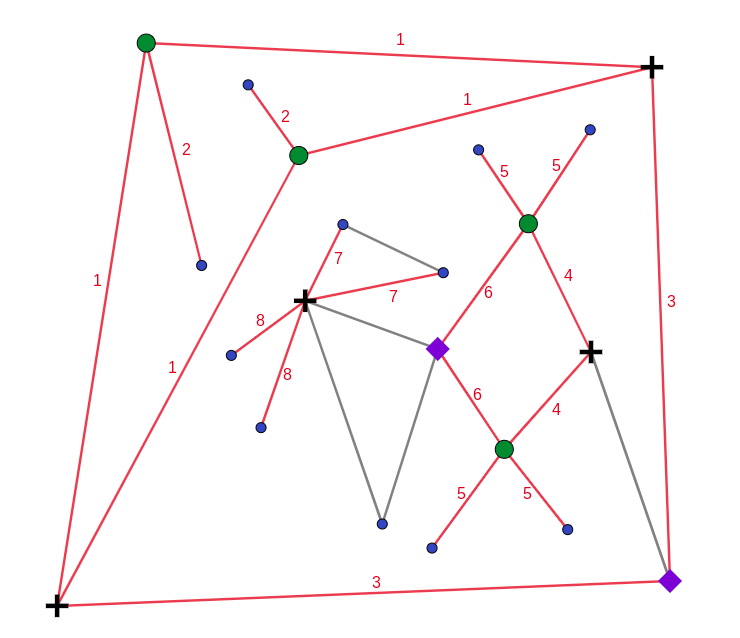
Bernard: I know Cheryl’s edge.
Similarly, this means B must be adjacent to a unique candidate for A (black cross). The only purple diamond adjacent to a unique black cross is the one belonging to the two red edges labelled “6”. In particular, this lets us conclude that Cheryl’s edge is the dashed blue edge in the following picture:
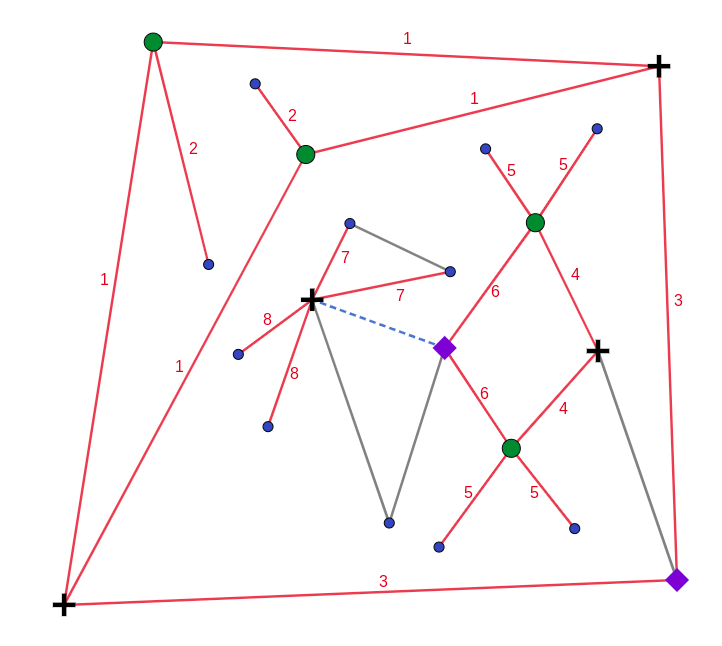
There are 8 edges in the graph that share exactly one endpoint with this edge.
Answer: edges = 8
nonogram
Since there are a very large number of 5-by-5 nonograms (approximately 225 ≈ 32M), we will not keep track of the set of possible nonograms explicitly. Instead, we will make several deductions about properties of the nonogram as we go along.
Albert: I don't know whether the first two columns of the grid have any filled-in squares.
If Albert doesn’t know whether the first two columns of the grid have any filled-in squares, it must be possible for all of Albert’s clues to fit within the last three columns of the grid (for example, the clue [1 1] fits within the last three columns of the grid, but the clue [2 2] does not). This means all of Albert’s clues must belong to the set {[0], [1], [2], [3], [1 1]}.
(Also, it cannot be the case that all of Albert’s clues are [0], but this will also become evident from other clues).
We will break Bernard’s next statement into three parts.
Bernard: I already knew you didn't know that.
How can Bernard possibly know that Albert’s clues all fit within the last three columns of the grid? One way this is possible is if Bernard knows that all the cells in the solution lie within a span of 3 consecutive columns; in other words, if Bernard’s 5 clues take the form (?, ?, ?, [0], [0]), ([0], ?, ?, ?, [0]), or ([0], [0], ?, ?, ?) where we use ? here to denote any possible clue. Another way it is possible is if Bernard has 2 or fewer non-zero clues; in this case regardless of the location of Bernard’s non-zero clues, all of Albert’s clues will belong to {[1 1], [2], [1], [0]} and therefore could fit within a span of three columns.
We next claim that the above characterization is necessary. In particular, if Bernard has at least 3 non-zero clues, then Bernard has exactly 3 non-zero clues and they are in a span of 3 consecutive columns (i.e. Bernard’s clues take one of the three forms listed above). If not, look at the locations of Bernard’s non-zero clues; if these non-zero clues span a set of columns of width > 3, then Bernard can imagine a consistent nonogram where one of Albert’s clues has width > 3, contradicting Albert’s earlier statement. For example, if Bernard’s clues were ([1 1] [0] [2 2] [3] [0]) then as far as Bernard knows at the very beginning of the conversation, the nonogram could be:
In this case, Albert’s first clue is [1 2], which does not fit within a span of width 3. In general, Bernard can perform this trick of shifting his non-zero clues as high up as possible and cause Albert’s first clue to have minimum width larger than 3.
Bernard: One of my clues is a 5.
We further know that one of these three non-zero columns is completely filled in. As a side-effect, we now know that Albert cannot have any [0] clues.
Bernard: I don't know if the filled-in squares form an orthogonally-connected region.
There are several deductions possible from this statement, but the most useful one is that the [5] cannot appear as the middle clue of the three non-zero columns — this is since if we place the [5] in the middle, no matter what we place on either side of the [5], the resulting set of black squares will be orthogonally-connected. Similarly, this rules out the possibility that there are fewer than 3 non-zero columns. We will also use the fact that this rules out the possibility that Bernard has two or more [5] clues; if so, the resulting region will be orthogonally-connected, no matter how we place the [5]s.
Before proceeding onto Albert’s next statement, let’s take stock of what Albert now knows about the nonogram — as we will soon see, Albert knows quite a bit.
We (and therefore Albert) know that:
- The filled-in squares of the nonogram fit into a smaller 5-by-3 region.
- In this 5-by-3 region, either the first column is completely filled in (and the last column is not), or the last column is completely filled in (and the first column is not).
From now on, call this smaller 5-by-3 region the subgrid. We now claim that Albert knows the contents of this subgrid almost uniquely — in fact, we will show that Albert has exactly two possibilities for the contents of this subgrid, and they are horizontal reflections (across some vertical line) of one another.
To see why, we claim that as soon as Albert fixes the location of the [5] in the subgrid, Albert can fill in the rest of the subgrid from his clues. In particular, recall that all of Albert’s clues belong to the set {[1], [2], [3], [1 1]}. For each of these clues, specifying the location of the left-most black square and the fact that they have to fit within a span of three columns allows us to uniquely place the black squares:
| [1] | |||
|---|---|---|---|
| [2] | |||
| [3] | |||
| [1 1] |
Similarly, specifying the location of the right-most black square and the fact that they have to fit within a span of three columns also allows us to uniquely place the black squares, and in fact doing so results in a horizontal reflection of the solution we get in the first case.
We have therefore shown that Albert knows the contents of the subgrid up to a horizontal reflection. Since the contents of the grid cannot be symmetric with respect to such a reflection (in particular, only one of the two side columns can be a [5]), Albert has exactly two possibilities for the content of the subgrid.
Finally, what does Albert know about the location of the subgrid? If we look at Bernard’s previous statement, we’ll see that so far, the answer is nothing — if Bernard’s statement is true for a specific nonogram, it is also true for the nonogram formed by shifting the subgrid horizontally in the main 5-by-5 grid. Since there are three possible 5-by-3 subgrids, this means that right now Albert has exactly 6 candidates for the solution to the nonogram.
Albert: I don't know if you know whether the center of the grid is filled in, but I know whether the center of the grid is filled in.
Let us first focus on the fact that Albert knows whether the center of the grid is filled in. As we have just established, Albert knows the contents of the subgrid up to reflection, but does not know the location of the subgrid in the main grid. If Albert’s center row is not a [3], then there is necessarily an empty square somewhere in the center row of the subgrid, and there is some translation of this subgrid which places this empty square at the very center of the grid. But similarly, since Albert’s center row is not a [0], there is necessarily a filled-in square somewhere in the center row of the subgrid, and it’s therefore also possible that the center is filled-in. It follows that the only way Albert can make this statement is if Albert’s middle clue is a [3]. Note that this means that Albert actually knows the stronger statement that the center of the grid is filled in.
Albert also does not know if Bernard knows whether the center of the grid is filled in. While it is possible to deduce some facts from this right now (for example, we can guarantee that Bernard’s two other clues apart from the [5] are not both [3]s), we’ll return to this fact later.
Bernard: I did not know whether the center of the grid was filled in, but I do now. In addition, I now know that the filled-in squares form an orthogonally-connected region. I don't know if you know the shape formed by this region (where two shapes are the same if they can be translated and rotated to match).
Again, Bernard is saying several different things in this clue. We’ll actually start with the last statement Bernard says — that Bernard does not know whether Albert knows the shape formed by the region of filled-in squares (up to rotation and translation).
This is an interesting statement, since as noted above, we (and thus Bernard) know that Albert does know the shape formed by this region up to reflection. Moreover, without rotation, we know that Albert has two candidate possibilities for the shape, since we know the shape is not symmetric with respect to a horizontal reflection, and nothing Bernard has said so far distinguishes this nonogram from its horizontal reflection.
So when is it the case that two distinct shapes that are (horizontal) reflections of each other can be transformed into one another by rotations / translations? The answer is when the shape possesses an axis of symmetry. Since we know our shape does not have horizontal symmetry, if it has this property, it must have vertical symmetry.
In particular, since Bernard does not know the shape formed by this region, Bernard must believe it is possible that the shape has vertical symmetry. In particular, it must be the case that each of Bernard’s clues has the potential to be symmetric about the center row. This rules out many possible clues for Bernard, and leaves only {[1], [3], [1 1], [1 1 1]} as possible clues (in addition to the [5] which we know occurs exactly once. In fact, we can further rule out [1 1], since Bernard also knows (as we do) that from Albert’s statements, the middle row of the subgrid is filled in. There is no way to place a [1 1] column clue symmetrically about the middle row while also filling in the middle square of the column. The remaining clues therefore must belong to the set {[1], [3], [1 1 1]}.
Let us now revisit the other parts of Bernard’s statement. Bernard begins by stating that he did not know whether the center of the grid was filled in, but he does now. This second bit (that he does now) conveys no information, since even we know that the center of the grid is filled in, but the fact that he did not originally tells us that whatever clue Bernard has for the center column (of the original grid, not the subgrid) must not reveal that the center is filled-in — in particular, it must be [1] (since [3] and [1 1 1] reveal this).
We now know two of Bernard’s clues are [1] and [5]. The remaining clue must be one of [1], [3], and [1 1 1]. In fact, Bernard’s sequence of three non-zero clues (up to reflection) must be one of ([5], [1], [1]), ([5], [1], [3]), ([5], [3], [1]), ([5], [1 1 1], [1]). (We eliminated ([5], [1], [1 1 1]) since this cannot possibly be connected).
Albert: I do not. In particular, I do not know whether the cell in row 4 column 2 is filled in (although I do know that all four corners of the grid are empty).
Albert does not know the shape, so Albert’s clues (and thus the shape) must not actually be vertically symmetric. Note that this rules out ([5], [1 1 1], [1]) from the above list. This also rules out ([5], [1], [1]) since if the center row of the subgrid is filled in, this pattern is necessarily vertically symmetric. We are therefore down to ([5], [3], [1]) and ([5], [1], [3]) (up to reflection, so ([1], [3], [5]) and ([3], [1], [5]) are also still possible).
Albert also tells us that all four corners of the grid are empty. Note that this is not possible if the pattern is ([5], [3], [1]) — if the pattern is ([5], [3], [1]) then in order for Bernard to not originally know whether the center is filled in, the [5] must occur in either the first column or last column, which would result in two corners being filled in. The clues for the subgrid are thus either ([5], [1], [3]) or ([3], [1], [5]), and the subgrid must be located in the middle three columns of the grid. Equivalently, Bernard’s five clues for the grid must either be ([0], [5], [1], [3], [0]) or ([0], [3], [1], [5], [0]).
Finally, we have our first bit of information that breaks symmetry — Albert states that he does not know whether the cell in row 4 column 2 is filled in. We will return to this bit of information shortly.
Bernard: Until you said that, I did not know whether the cell in row 4 column 2 was filled in, but now I know the solution to the nonogram.
Bernard tells us that he also did not originally know whether the cell in row 4 column 2 was filled in. If Bernard’s clues are ([0], [5], [1], [3], [0]) he knows that all of column 2 is filled in, so Bernard’s clues must be ([0], [3], [1], [5], [0]).
There are only three nonograms consistent with this set of Bernard’s clues and the fact that the center is filled in:
In the latter two of these, Albert’s clue for row 4 is [1 1], and therefore Albert (in combination with the knowledge that the subgrid spans the middle three columns) knows that row 4 column 2 is filled in. It follows that the only possible nonogram is the first of these, namely:
This nonogram depicts the digit 4.
Answer: nonogram = 4
state
The state abbreviations of all 50 states are summarized by the black squares in the following table (where the row corresponds to the first letter of the state abbreviation, and the column corresponds to the second letter of the state abbreviation):
| A | C | D | E | H | I | J | K | L | M | N | O | R | S | T | V | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | x | x | x | x | |||||||||||||||
| C | x | x | x | ||||||||||||||||
| D | x | ||||||||||||||||||
| F | x | ||||||||||||||||||
| G | x | ||||||||||||||||||
| H | x | ||||||||||||||||||
| I | x | x | x | x | |||||||||||||||
| K | x | x | |||||||||||||||||
| L | x | ||||||||||||||||||
| M | x | x | x | x | x | x | x | x | |||||||||||
| N | x | x | x | x | x | x | x | x | |||||||||||
| O | x | x | x | ||||||||||||||||
| P | x | ||||||||||||||||||
| R | x | ||||||||||||||||||
| S | x | x | |||||||||||||||||
| T | x | x | |||||||||||||||||
| U | x | ||||||||||||||||||
| V | x | x | |||||||||||||||||
| W | x | x | x | x |
Albert: I don’t know the state.
Albert’s row of the table must contain at least 2 black squares. This lets us eliminate rows D, F, G, H, L, P, R, and U.
| A | C | D | E | H | I | J | K | L | M | N | O | R | S | T | V | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | x | x | x | x | |||||||||||||||
| C | x | x | x | ||||||||||||||||
| I | x | x | x | x | |||||||||||||||
| K | x | x | |||||||||||||||||
| M | x | x | x | x | x | x | x | x | |||||||||||
| N | x | x | x | x | x | x | x | x | |||||||||||
| O | x | x | x | ||||||||||||||||
| S | x | x | |||||||||||||||||
| T | x | x | |||||||||||||||||
| V | x | x | |||||||||||||||||
| W | x | x | x | x |
Bernard: I don't know the state.
Similarly, Bernard’s column of the table must contain at least 2 black squares. This lets us eliminate columns J, M, X, and Z.
| A | C | D | E | H | I | K | L | N | O | R | S | T | V | Y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | x | x | x | ||||||||||||
| C | x | x | x | ||||||||||||
| I | x | x | x | x | |||||||||||
| K | x | x | |||||||||||||
| M | x | x | x | x | x | x | x | x | |||||||
| N | x | x | x | x | x | x | |||||||||
| O | x | x | x | ||||||||||||
| S | x | x | |||||||||||||
| T | x | ||||||||||||||
| V | x | x | |||||||||||||
| W | x | x | x | x |
Albert: I don't know the state.
Albert’s row of the table must again contain at least 2 black squares. This lets us eliminate row T. Before we eliminate it, let’s consider the next two statements as well.
Bernard: I already knew that.
Bernard already knew that Albert didn’t know the state — in other words, Bernard already knew that Albert’s letter is not T. Since TN is the only state abbreviation where it is possible for Albert’s letter to be T, this means that we can eliminate column N for Bernard.
Albert: Well I already knew that you already knew that.
Albert already knew that Bernard already knew that Albert didn’t know the state. From the above logic, this means that Albert already knew that Bernard’s letter was not N. Since IN and MN are also states, this means that Albert cannot have the letter I or M.
All in all, this lets us eliminate rows I, M, and T for Albert, and column N for bernard.
| A | C | D | E | H | I | K | L | O | R | S | T | V | Y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | x | x | x | |||||||||||
| C | x | x | x | |||||||||||
| K | x | x | ||||||||||||
| N | x | x | x | x | x | x | ||||||||
| O | x | x | x | |||||||||||
| S | x | x | ||||||||||||
| V | x | x | ||||||||||||
| W | x | x | x | x |
Bernard: I still don't know what the state is.
We can eliminate columns with a unique black square. This allows us to eliminate columns E, I, L, O, and S.
| A | C | D | H | K | R | T | V | Y | |
|---|---|---|---|---|---|---|---|---|---|
| A | x | x | |||||||
| C | x | x | |||||||
| K | x | ||||||||
| N | x | x | x | x | x | ||||
| O | x | x | x | ||||||
| S | x | x | |||||||
| V | x | x | |||||||
| W | x | x | x |
Albert: I also don't know what the state is.
We can eliminate rows with a unique black square. This allows us to eliminate row K.
| A | C | D | H | K | R | T | V | Y | |
|---|---|---|---|---|---|---|---|---|---|
| A | x | x | |||||||
| C | x | x | |||||||
| N | x | x | x | x | x | ||||
| O | x | x | x | ||||||
| S | x | x | |||||||
| V | x | x | |||||||
| W | x | x | x |
Bernard: Again, I still don't know the state.
Again, we can eliminate columns with a unique black square, but no such columns exist.
Albert: Well, I don't even know how many states you still think are possibly the correct state.
The number of states Bernard possibly thinks are the correct state is equal to the number of black squares in Bernard’s column. We therefore want to eliminate rows where each black square in the row contains the same number of black squares in its column.
By inspection, this is true for rows A, N, O, and S, which we now eliminate (along with columns left with 0 remaining black squares).
| A | T | V | Y | |
|---|---|---|---|---|
| C | x | x | ||
| V | x | x | ||
| W | x | x | x |
Bernard: Well, I know how many possibilities you have narrowed down the state to.
Similarly, we now want to eliminate columns where each black square in the column does not appear the same number of times in its row. This eliminates column A.
| T | V | Y | |
|---|---|---|---|
| C | x | ||
| V | x | ||
| W | x | x |
Albert: I now know the state. By the way, the state does not border Canada.
Since Albert knows the state, Albert’s row is C or V and the state is either CT or VT. Of these two states, Vermont (VT) borders Canada, whereas Connecticut (CT) does not, so the answer to this puzzle is CT. (The remaining line of dialogue conveys no further information).
Answer: CT
sum and product
Albert: I don’t know whether you know my number.
Before this statement, Bernard knows Albert’s number if and only if Bernard’s number is a prime p (which would allow him to deduce that the set is {1, p} and that Albert’s number is 1 + p) or a square of a prime p2 (which would allow him to deduce that the set is {1, p2} and that Albert’s number is 1 + p2). (Note that Bernard’s number can never be 1, which is not the product of two or more distinct positive integers.) Any other number n has a nontrivial factorization n = pq where p and q are distinct integers > 1, and Bernard would not be able to distinguish between {1, pq} and {p, q}. So, if Albert believes it’s possible that Bernard knows Albert’s number, we know that Albert’s number is of the form 1 + p or 1 + p2.
We can further eliminate some small cases for Albert’s number. If Albert’s number is 3, Albert can deduce that the set is {1, 2} and that Bernard’s number is 2, which is also enough to deduce the set. In this case Albert would know that Bernard knows Albert’s number, which is impossible.
Similarly, if Albert’s number is 4, Albert can deduce that the set is {1, 3} and that Bernard’s number is 3, which is also enough to deduce the set, so this case can be eliminated as well.
Larger numbers are still consistent, however: If Albert has 5, the set could be {1, 4} or {2, 3}, making Bernard’s number 4 or 6. If Albert has 6, the set could be {1, 5}, {2, 4}, or {1, 2, 3}, making Bernard’s number 5, 8, or 6. Larger numbers give even more possibilities for the set and for Bernard’s number.
Bernard: I know your number, and now I know you know my number too.
We’ve already eliminated Albert’s number being 3 or 4. We can check that, if the set is {1, 4} so that Albert’s number is 5 and Bernard’s number is 4, everything is consistent:
- As above, from Albert’s initial point of view, the set could be {1, 4} or {2, 3}; Bernard would start out knowing Albert’s number in the former case but not the latter.
- If the set were actually {2, 3}, Albert stating that he doesn’t know whether Bernard knows his number does not allow Bernard to distinguish between {2, 3} and {1, 2, 3}, so Bernard cannot say that he knows Albert’s number after the first statement.
- With the set actually being {1, 4}, however, Bernard can immediately deduce that the set is {1, 4} even before Albert’s first statement.
- Therefore, Bernard stating that he knows Albert’s number allows Albert to deduce Bernard’s number, which Bernard also knows, and the conversation is fully consistent.
If Albert’s number is none of the above, it’s at least 6 and is one more than either an odd prime or the square of an odd prime, so it must be an even number ≥ 6.
If it’s 6, we can actually check that when Bernard’s number is either 5 or 8, Bernard can deduce the set and Albert’s number:
- 5 is definitely {1, 5}.
- 8 could be {1, 8}, {2, 4}, or {1, 2, 4}, producing sums 9, 6, and 7. Of these, only 6 is one more than a prime or the square of a prime.
Otherwise, Albert’s number is an even number greater than 6, and we know that it’s less than 4 × 1018. Let it be A. Here we will lean on empirical verification of a slightly strengthened version of Goldbach’s conjecture, and write A as the sum of two distinct primes q + r. Now:
- If Bernard’s number were A − 1 (which is a prime or square of a prime), the set would be {1, A − 1} and Bernard would know Albert’s number.
- But if Bernard’s number were qr, Bernard could still conclude that the set is either {q, r} or {1, qr}. However, Bernard can eliminate the second case using Albert’s first statement, as 1 + qr is not in fact one more than a prime or a square prime, and he would know Albert’s number.
Therefore, there are at least two possible values of Bernard’s number that would enable him to say that Bernard knows Albert’s number, so Albert cannot know Bernard’s number after the first half of Bernard’s statement, and Bernard certainly could not conclude that either.
We have therefore eliminated all cases except the set {1, 4}, where Albert gets 5 and Bernard gets 4.
Answer: sum = 5, product = 4
whether
Before we start examining the conversation between Albert and Bernard, let’s attempt to better understand what statements like “Albert knows whether Bernard knows whether Albert knows the numbers” imply about the numbers given to Albert and Bernard.
As in the puzzle description, assume that Albert and Bernard are given positive integers a and b respectively such that either a = b or a = b + 1 (for now we will not worry about the upper bound on a and b). We will now define a statement W(n) for each non-negative integer n ≥ 0, such that the statement W(n) contains n “whether”s. Let W(0) be the statement “Albert knows Bernard’s number”. Now for any n > 0, let W(n) be the statement “Bernard knows whether W(n−1) is true” if n is odd, and let W(n) be the statement “Albert knows whether W(n−1) is true” if n is even. The first couple statements W(n) can be written out as follows:
- W(0): “Albert knows Bernard’s number.”
- W(1): “Bernard knows whether Albert knows Bernard’s number.”
- W(2): “Albert knows whether Bernard knows whether Albert knows Bernard’s number.”
- …
What does the statement W(n) imply about a and b? To start, note that W(0) implies that a = 1 (and b = 1), since this is the only setting where Albert knows Bernard’s number uniquely. Given this, we can reinterpret W(1) as “Bernard knows whether a = 1”. If b > 1, then Bernard knows that a cannot possibly be 1; however if b = 1, a could be either 1 or 2 (so Bernard does not know the truth of W(0)). In particular, W(1) implies that b ≠ 1.
Similarly, we can reinterpret W(2) as “Albert knows whether b ≠ 1”. Certainly if a = 1, Albert knows that b = 1 (and therefore whether b ≠ 1). Similarly, if a > 2, Albert knows that b > 1, and thus knows that b ≠ 1. However, if a = 2, Albert does not know if b = 1 or 2. W(2) therefore implies that a ≠ 2.
We can continue onwards to figure out the implication of W(n) for ever increasing values of n. More succinctly, for each value of W(n), we learn either that a cannot belong to some set of values S(n) (if n is even), or that b cannot belong to some set of values S(n) (if n is odd). Moreover, the rule for constructing S(n) from S(n−1) is relatively simple:
- If n is even, then S(n) contains all numbers x > 1 such that exactly one of x and x−1 belong to S(n−1) (this is the set of values for a forbidden by the statement “Albert knows whether b belongs to S(n−1)”).
- If n is odd, then S(n) contains all numbers x > 0 such that exactly one of x and x+1 belong to S(n−1) (this is the set of values for b forbidden by the statement “Bernard knows whether a belongs to S(n−1)”).
This lets us quickly construct the following table of sets S(n) (where a cell is filled-in if the corresponding element belongs to S(n)):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S(1) | |||||||||||
| S(2) | |||||||||||
| S(3) | |||||||||||
| S(4) | |||||||||||
| S(5) | |||||||||||
| S(6) | |||||||||||
| S(7) | |||||||||||
| S(8) | |||||||||||
| S(9) | |||||||||||
| S(10) | |||||||||||
| S(11) | |||||||||||
| S(12) | |||||||||||
| S(13) | |||||||||||
| S(14) | |||||||||||
| S(15) | |||||||||||
| S(16) | |||||||||||
| S(17) | |||||||||||
| S(18) | |||||||||||
| S(19) | |||||||||||
| S(20) |
(Observant solvers might notice that drawing out this table results in a fractal pattern similar to half of Sierpinski’s triangle).
We are now ready to analyze the conversation between Albert and Bernard.
Albert: I know whether you know my number.
Bernard knows Albert’s number only if b = 11, so we know that a ≠ 11.
Bernard: I know whether you know my number.
Albert knows Bernard’s number only if a = 1, so we know that b ≠ 1.
Albert: I know whether you know my number.
We have a repeat of the first line, except now we (and Albert and Bernard) know that a≠ 11 and b ≠ 1. This is equivalent to Cheryl originally choosing numbers between 2 and 10 inclusive for Albert and Bernard. It similarly follows that this implies that a ≠ 10.
Bernard: I know whether you know whether I know whether you know whether I know whether you know whether I know whether you know whether I know whether you know whether I know whether you know whether I know whether you know my number.
We can verify that this statement is equivalent to W(13). Since we know that b ≠ 1, and a ≠ 10, 11, if we let a’ = a − 1 and b’ = b − 1, we can instead pretend that Cheryl gave Albert and Bernard numbers a’ and b’ between 1 and 8 inclusive with the property that either a’ = b’ or a’ = b’+ 1.
Reading off S(13) from the above table, we know that W(13) implies that b’ cannot equal 2, 3, 6, or 7. In particular, this means that b cannot equal 3, 4, 7, or 8.
Albert: I don't know your number.
We now have the following remaining options for a and b. We know that b cannot equal 1, 3, 4, 7, or 8. We also know that a cannot equal 10 or 11. Together, this means that (a, b) must be one of (2, 2), (3, 2), (5, 5), (6, 5), (6, 6), (7, 6), or (9, 9). Of these possibilities, the only cases in which Albert cannot uniquely identify Bernard’s number are if a = 6 and b = 5 or 6. It follows that Albert’s number is 6.
Answer: whether = 6
whisper1 and whisper2
At the beginning of this part of the puzzle, Cheryl whispers information to Albert. Afterward, Albert knows the exact value of whisper1 and may additionally have some information about the value of whisper2. We’ll approach this part of the puzzle by considering all possibilities for what Albert may know about the pair (whisper1, whisper2).
Albert: I don’t know your number.
At this point, there are nine possibilities for what Albert may know about the pair (whisper1, whisper2). Let us call them 1(a, b, c, d), 2(a, b, c, d), and 3. They are as follows.
- whisper1 = 1
- Albert knows that whisper1 = 1, and he knows (from what Cheryl whispered to him) that whisper2 is 1 or 2.
- Albert knows that whisper1 = 1, and he knows that whisper2 is 2 or 3.
- Albert knows that whisper1 = 1, and he knows that whisper2 is 1 or 3.
- Albert knows that whisper1 = 1, and the information Cheryl whispered to Albert told him nothing about the value of whisper2. So, Albert only knows that whisper2 can be 1, 2, or 3.
- whisper1 = 2
- Albert knows that whisper1 = 2, and he knows that whisper2 is 2 or 3.
- Albert knows that whisper1 = 2, and he knows that whisper2 is 3 or 4.
- Albert knows that whisper1 = 2, and he knows that whisper2 is 2 or 4.
- Albert knows that whisper1 = 2, and he knows that whisper2 is 2, 3, or 4.
- whisper1 = 3
- Albert knows that whisper1 = 3, and he knows that whisper2 is 1 or 5.
These possibilities can be summarized in a table similar to the ones used in previous parts of this solution. The columns of the table correspond to the nine possibilities listed above (Albert’s knowledge), and the rows of the table correspond to the five possible values of whisper2 (Bernard’s knowledge). The white cells correspond to the possible states of Albert’s and Bernard’s knowledge.
| 1(a) | 1(b) | 1(c) | 1(d) | 2(a) | 2(b) | 2(c) | 2(d) | 3 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 |
Bernard: Then you don’t know whether my number is greater than your number.
Albert knows whether whisper2 > whisper1 in exactly scenarios 1(b) and 2(b). So we remove rows 2, 3, and 4 of the table, because they contain a white cell in column 1(b) or 2(b). Let’s also clean up the columns that have no remaining white cells.
| 1(a) | 1(c) | 1(d) | 3 | |
|---|---|---|---|---|
| 1 | ||||
| 5 |
Albert: I now know your number.
We now remove any column that contains more than one white cell, leaving only the possibility that whisper1 = 1 and whisper2 = 1.
Answer: whisper1 = 1, whisper2 = 1
Solution to the meta puzzle
By substituting in the answers from all the subpuzzles, we obtain the following conversation.
Albert: I don't know if the answer contains exactly 4 vowels.
Bernard: I don't know if the answer contains exactly 4 vowels.
Albert: I don't know if the answer contains CT as a substring.
Bernard: I don't know if the answer contains CT as a substring.
Albert: I don't know if the sum of the 1st and 5th letters (where A=1, B=2, ...) is at least 8.
Bernard: I don't know if the sum of the 1st and 5th letters (where A=1, B=2, ...) is at least 10.
Albert: I don’t know if the Scrabble score of the answer is equal to 8.
Bernard: I don’t know if the Scrabble score of the answer is equal to 6.
Albert: I don't know if the set of letters in the answer contains 4 consecutive letters.
Bernard: I don't know if the set of letters in the answer contains 4 consecutive letters.
Albert: I don’t know if the 1st letter, the 3rd letter, and the 6th letter of the answer form a common English word when concatenated.
Bernard: I don’t know if the 6th letter, the 1st letter, and the 4th letter of the answer form a common English word when concatenated.
Albert: I don’t know if the product of all the letters (where A=1, B=2, ...) in the answer is divisible by 32.
Cheryl: Oh, I forgot to tell you this earlier, but all the letters in the answer are distinct.
Bernard: I know the answer to this puzzle.
Albert: I know the answer to this puzzle.
We now proceed as usual.
Albert: I don't know if the answer contains exactly 4 vowels.
The only way Albert is sure that the answer does not contain exactly 4 vowels is if Albert’s trigram contains no vowels. It follows that Albert’s trigram must contain a vowel.
Bernard: I don't know if the answer contains exactly 4 vowels.
Similarly, this is possible if and only if Bernard’s trigram contains at least one vowel (even though Bernard knows that Albert’s trigram contains at least one vowel, Bernard’s trigram could still contain 1, 2, or 3 vowels and satisfy the constraint that the answer contains 4 vowels).
Albert: I don't know if the answer contains CT as a substring.
This implies that Albert’s trigram does not contain CT as a substring. If Albert’s trigram does not contain CT, then CT can still occur as a substring of the answer either by occurring entirely within Bernard’s trigram or occurring across trigram boundaries (as the 3rd and 4th letters).
Bernard: I don't know if the answer contains CT as a substring.
Again, this implies that Bernard’s trigram does not contain CT as a substring. Furthermore, since Bernard knows that Albert’s trigram does not contain CT as a substring, it must be possible for CT to appear across trigram boundaries. This implies that the fourth letter of the answer (and the first letter of Bernard’s trigram) is a T.
Summarizing, so far we know that Albert’s trigram is ??? (one letter of which must be a vowel), and Bernard’s trigram is T?? (one letter of which must be a vowel).
Albert: I don't know if the sum of the 1st and 5th letters (where A=1, B=2, ...) is at least 8.
As far as Albert knows, the 5th letter can be any letter. In order for the sum to possibly be below 8, this means that the value of the first letter must be between 1 and 6, so the first letter of the answer is between A and F inclusive.
[A-F]??, T??
Bernard: I don't know if the sum of the 1st and 5th letters (where A=1, B=2, ...) is at least 10.
Bernard knows that the first letter has value between 1 and 6. In order for it to be possible for the sum to both be below 10 and at least 10, the fifth letter of the answer (Bernard’s second letter) must be between 4 and 8 in value. The fifth letter is thus between D and H inclusive.
[A-F]??, T[D-H]?
Albert: I don’t know if the Scrabble score of the answer is equal to 8.
It is useful here to recall the mapping from letters to Scrabble values:
- 1 point: A, E, I, O, U, L, N, S, T, R
- 2 points: D, G
- 3 points: B, C, M, P
- 4 points: F, H, V, W, Y
- 5 points: K
- 8 points: J, X
- 10 points: Q, Z
Note that there are very few possible ways a six-letter word can have a Scrabble score of 8; either it must contain five 1-point letters and one 3-point letter, or four 1-point letters and two 2-point letters. In particular, if Albert makes this claim, it is not possible for any of his letters to be worth 4 or more points (and as long as all of his letters are worth at most 5 points total, it is possible that this constraint is satisfied). In particular, Albert’s first letter cannot be F.
[A-E]??, T[D-H]?
Bernard: I don’t know if the Scrabble score of the answer is equal to 6.
This is an even stronger statement — it implies that all of the letters in Bernard’s trigram must be worth 1 point. This is true for the T, but reduces the possibilities for the second letter of Bernard’s trigram to just E.
[A-E]??, TE?
Albert: I don't know if the set of letters in the answer contains 4 consecutive letters.
Let us think about the possible ways in which the answer can contain 4 consecutive letters. Any such streak of 4 consecutive letters must contain letters from both trigrams. Moreover, since the fourth and fifth letters (the T and the E) cannot belong to the same streak of length 4, this streak must contain at least two letters from Albert’s trigram.
Let’s first consider the case where the streak contains 3 letters from Albert’s trigram. Then the streak must contain a letter between A and E, so it must be one of ABCD, BCDE, CDEF, DEFG, or EFGH. However, since we can have at most one 3-point value letter and at most two 2-point value letters in our answer (and no letters of higher value), this rules out all these possibilities.
The streak must then contain 2 letters from Albert’s trigram and 2 letters from Bernard’s trigram. As previously mentioned, the two letters from Bernard’s trigram cannot be the fourth and fifth letters. Let us now consider the case that they are the fifth and sixth letters (i.e. the E and the ?). However, this case is impossible, since all streaks of length 4 containing an E have too high of a scrabble value.
It follows that the streak must contain the fourth and sixth letters from Bernard’s trigram, and (since the fourth letter is a T) be one of QRST, RSTU, STUV, TUVW. Of these choices, all have too high of a Scrabble value except for RSTU. Finally, since the first letter must be between A and E, the streak must contain the second and third letters (and therefore the second, third, fourth, and sixth letters must be RSTU in some order). In fact, since the fourth letter is the T, the second, third, and sixth letters must be RSU in some order.
Importantly, this means that as long as Albert’s second and third letters are two distinct letters from the set [RSU], it is possible that the answer contains 4 consecutive letters.
[A-E][RSU][RSU], TE?
Bernard: I don't know if the set of letters in the answer contains 4 consecutive letters.
By following the above logic, Bernard also knows that the only way the answer can contain 4 consecutive letters is if it contains all the letters in RSTU. From Albert’s previous statement, Bernard knows that Albert has two of the letters in the set {R, S, U} as his second and third letter. In order for it to be possible that the answer contains 4 consecutive letters, Bernard must also have a letter in the set {R, S, U} as his third letter (and as the answer’s sixth letter).
[A-E][RSU][RSU], TE[RSU]
Albert: I don’t know if the 1st letter, the 3rd letter, and the 6th letter of the answer form a common English word when concatenated.
There are fifteen possibilities for the bigram formed by the first and third letters of the answer: AR, AS, AU, BR, BS, BU, CR, CS, CU, DR, DS, DU, ER, ES, and EU. For each of these possibilities, let us look at whether it is possible for it to form a common English word when concatenated with the sixth letter (which is one of R, S, and U):
- AR: None of ARR, ARS, and ARU are common English words.
- AS: ASS is a common English word (the other two possibilities are not).
- AU: None of AUR, AUS, and AUU are common English words.
- BR: None of BRR, BRS, and BRU are common English words.
- BS: None of BSR, BSS, and BSU are common English words.
- BU: BUR and BUS are common English words, but BUU is not.
- CR: None of CRR, CRS, and CRU are common English words.
- CS: None of CSR, CSS, and CSU are common English words.
- CU: CUR is a common English word (the other two possibilities are not).
- DR: None of DRR, DRS, and DRU are common English words.
- DS: None of DSR, DSS, and DSU are common English words.
- DU: None of DUR, DUS, and DUU are common English words.
- ER: ERR is a common English word (ERS is probably not a common English word, and ERU is definitely not a common English word).
- ES: ESS is a common English word (the other two possibilities are not).
- EU: None of EUR, EUS, and EUU are common English words.
This bigram therefore must be one of AS, BU, CU, ER, or ES. In particular, the first letter cannot be D.
[ABCE][RSU][RSU], TE[RSU]
Bernard: I don’t know if the 6th letter, the 1st letter, and the 4th letter of the answer form a common English word when concatenated.
Bernard knows that the 6th letter is one of R, S, or U, and that the 4th letter is T. If the 6th letter is R, then Bernard knows it is possible for this concatenation to be RAT (which is a common English word) and also possible for it to be RBT (which is not a common english word). If the 6th letter is S, then Bernard knows it is possible for this concatenation to be SAT (a common English word) and also for it to be SBT (not a common English word).
However, if the 6th letter is U, then no matter the choice of first letter in {A, B, C, E}, this concatenation will not form an English word — it will form one of UAT, UBT, UCT, and UET. It follows that the 6th letter cannot be U.
[ABCE][RSU][RSU], TE[RS]
Albert: I don’t know if the product of all the letters (where A=1, B=2, ...) in the answer is divisible by 32.
Albert knows that Bernard’s trigram is either TER, with product 20 × 5 × 18 = 23 × 32 × 52, or TES, with product 20 × 5 × 19 = 22 × 52 × 19. In order for Albert to not know whether the product of all the letters is divisible by 32, the highest power of two dividing Albert’s trigram must be exactly 4; then if Bernard’s trigram is TER, the overall product is divisible by 32, and if Bernard’s trigram is TES, the overall product is not divisible by 32.
Now, the only possible even-valued letters in Albert’s trigram are B (with value 2), which can occur in the first position, and R (with value 18) which can occur in the second or third position (but not both, since the second and third letters must be distinct elements of {R, S, U}). Since both B and R just contribute a single power of 2 to the product, they must both appear in Albert’s trigram — in particular, Albert’s trigram begins with the letter B.
From our earlier analysis of bigrams, we know that if the first letter of the answer is B, the third letter of the answer must be U. Since R must appear somewhere in Albert’s trigram, the second letter of the answer is R.
BRU, TE[RS]
Cheryl: Oh, I forgot to tell you this earlier, but all the letters in the answer are distinct.
There are now exactly two possibilities available for the answer: BRUTES and BRUTER. Since Cheryl now tells us that all the letters are distinct, we can conclude (along with Albert and Bernard) that the answer to this puzzle is BRUTES.