Ignorance
View Solution
Show canned hints
| Keywords | Content |
|---|---|
(This puzzle probably isn't amenable to canned hints. Give hints to teams based on their progress.) |
|
birthday: This subpuzzle is isomorphic to the original Cheryl's birthday problem. If you understand the solution to that problem (which is easy to find online), you should be able to solve this subpuzzle. |
|
The first few steps of this puzzle are similar to deductions made in the original Cheryl's birthday problem. When Albert says "We could continue this conversation indefinitely", that should narrow the set of possible cells (from your perspective) from 15 to 10. |
|
d1, d2, d3: The first and third statements together produce a fairly strong implication about Cheryl's number, after which you should be able to produce a table that the remaining statements can be applied manageably to. |
|
div1 and div2: The table of possible number pairs given to Albert and Bernard is fairly small. You can probably make the full table and perform deductions on it. |
|
edges: The most useful first step is likely to label all equivalence classes of edges that cannot be distinguished by connectivity information alone. For example, the two edges that connect a vertex of degree 1 to a vertex of degree 3 near the top-left are indistinguishable. You should have 8 nontrivial equivalence classes, six of size 2 and two of size 4. The statements can be interpreted as assertions involving these equivalence classes. (this is a bad hint please fix it) |
|
nonogram: oh god why |
|
states: Though intimidating, the sequence of statements makes the most sense if you perform it as steps on a large 19x19 table with 50 filled-in squares and eliminate rows/columns. |
|
Sum and product: For the first step, try describing the mathematical property corresponding to whether Bernard's number enables him to know Albert's number right away. This lets you describe the set of numbers that Albert's number can be. Large numbers can be eliminated by relying on a certain conjecture that's been empirically verified for many numbers. This subpuzzle also isn't too hard to short-circuit; Albert and Bernard's numbers are very small and uniquely determined by the puzzle, so once you find a pair that works you can trust that they are the right numbers. |
|
whether: Consider the sequence of statements that starts: - W(0): “Albert knows Bernard’s number.” Try writing a recurrence that describes the set of possibilities implied by each statement. If you make a table it should make a pretty fractal pattern. |
|
whisper: Try making a table where the columns are all of Albert's possible states of knowledge after the first statement (there are nine). Then figure out which of them are states that tell Albert whether Bernard's number is larger. |
Albert and Bernard have just become friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates:
| May | 9 | 10 | ||||
|---|---|---|---|---|---|---|
| June | 8 | 11 | 12 | |||
| July | 11 | 12 | 13 | |||
| August | 8 | 10 |
Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively.
Albert: I don’t know when Cheryl’s birthday is, but I know that
Bernard doesn’t know too.
Bernard: At first I didn’t know when Cheryl’s birthday is, but I
know now.
Albert: Then I also know when Cheryl’s birthday is.
Let birthmonth be the month of Cheryl’s birthday (as a number from 1–12) and birthday be the day of Cheryl’s birthday.
| 30 | |||||||||
| 40 | 4 | 33 | 22 | 16 | |||||
| 35 | 3 | 32 | |||||||
| 17 | 18 | ||||||||
| 11 | |||||||||
| 14 | 31 | ||||||||
| 21 | 13 | ||||||||
| 15 | |||||||||
| 12 | 20 | 34 | |||||||
| 26 | 9 | 23 |
Cheryl picks a cell of the above 10-by-10 table containing a number. Cheryl tells which row the cell is in to Albert and which column the cell is in to Bernard. The above table is known to both Albert and Bernard.
Albert: I don’t know the location of the cell.
Bernard: I don’t know the location of the cell.
Albert: I don’t know the location of the cell.
Bernard: I don’t know the location of the cell.
Albert: We could continue this conversation indefinitely (by repeatedly
saying “I don’t know the location of the cell”) without
either of us learning the location of the cell.
Bernard: I know the location of the cell.
Let cell be the number written in Cheryl’s cell.
Denise is visiting town. She chooses 3 numbers between 1 and 6 inclusive and calls them d1, d2, and d3. She gives d2 + d3 to Albert, d1 + d3 to Bernard, and d1 + d2 to Cheryl.
Cheryl: I don’t know if there are exactly two 1s among Denise’s
three numbers.
Bernard: I don’t know if there are exactly zero 1s among
Denise’s three numbers.
Cheryl: I don’t know if there are exactly two 6s among Denise’s
three numbers.
Albert: I don’t know if there are exactly zero 6s among Denise’s
three numbers.
Bernard: I don’t know if there is exactly one 1 among Denise’s
three numbers.
Albert: I don’t know if there is exactly one 6 among Denise’s
three numbers.
Bernard: The number I was given is even.
Albert: The number I was given is prime.
Bernard: I now know Denise’s three numbers.
Cheryl gives Bernard a number between 1 and 7, and then gives Albert a proper divisor of Bernard’s number.
Albert: Bernard doesn’t know my number.
Albert: Bernard still doesn’t know my number.
Bernard: I now know Albert’s number.
Let div1 and div2 be Albert’s number and Bernard’s number respectively.
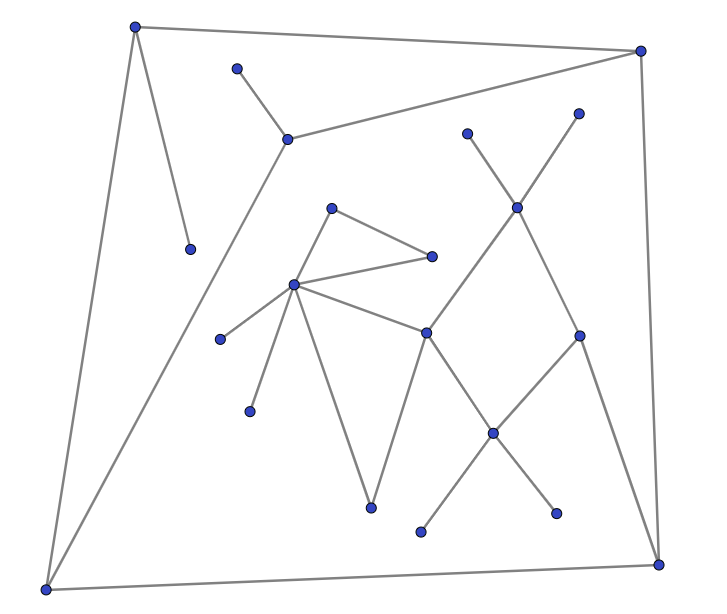
Cheryl draws the above graph (unknown to Albert and Bernard) and picks an edge from it. Cheryl gives this drawing and one of the endpoints of this edge to Albert. Cheryl then arbitrarily rearranges the vertices of this graph (producing an isomorphic graph). Cheryl gives this new drawing to Bernard, along with the identity of the other endpoint of her edge.
Albert: I don’t know if there’s any conversation we can have
where I will learn which edge is Cheryl’s edge.
Bernard: I don’t know if there’s any conversation we can have
where I will learn which edge is Cheryl’s edge.
Albert: I know Cheryl’s edge.
Bernard: I know Cheryl’s edge.
Let edges be the number of edges in the graph that share exactly one endpoint with Cheryl’s edge.
Albert and Bernard are solving a 5-by-5 nonogram. Albert has the clues for the 5 rows and Bernard has the clues for the 5 columns.
Albert: I don’t know whether the first two columns of the grid have any
filled-in squares.
Bernard: I already knew you didn’t know that. One of my clues is a 5. I
don’t know if the filled-in squares form a single orthogonally-connected
region.
Albert: I don’t know if you know whether the center of the grid is filled
in, but I know whether the center of the grid is filled in.
Bernard: I did not know whether the center of the grid was filled in, but I
do now. In addition, I now know that the filled-in squares form a single
orthogonally-connected region. I don’t know if you know the shape formed
by this region (where two shapes are the same if they can be translated and
rotated to match).
Albert: I do not. In particular, I do not know whether the cell in row 4
column 2 is filled in (although I do know that all four corners of the grid
are empty).
Bernard: Until you said that, I did not know whether the cell in row 4
column 2 was filled in, but now I know the solution to the nonogram.
Albert: I too now know the solution to this nonogram.
Let nonogram be the number depicted in the solution to this nonogram.
Cheryl picks her favorite U.S. state. Cheryl gives the first letter of the state abbrevation to Albert and the second letter of the state abbreviation to Bernard.
Albert: I don’t know the state.
Bernard: I don’t know the state.
Albert: I don’t know the state.
Bernard: I already knew that.
Albert: Well I already knew that you already knew that.
Bernard: I still don’t know what the state is.
Albert: I also don’t know what the state is.
Bernard: Again, I still don’t know the state.
Albert: Well, I don’t even know how many states you still think are
possibly the correct state.
Bernard: Well, I know how many possibilities you have narrowed down the
state to.
Albert: I now know the state. By the way, the state does not border
Canada.
Bernard: Thanks. I also now know the state.
Let state be the state abbreviation of Cheryl’s favorite state.
Cheryl picks a set of distinct positive integers with at least two elements, tells Albert this set’s sum, and tells Bernard this set’s product.
Albert: I don’t know whether you know my number.
Bernard: I know your number, and now I know you know my number too.
Albert: I do. Isn’t it convenient that both of our numbers are less
than 4,000,000,000,000,000,000?
Let sum be Albert’s number and product be Bernard’s number.
Cheryl gives Albert and Bernard numbers between 1 and 11 (inclusive) such that Albert’s number is either the same as Bernard’s number or one greater than Bernard’s number.
Albert: I know whether you know my number.
Bernard: I know whether you know my number.
Albert: I know whether you know my number.
Bernard: I know whether you know whether I know whether you know whether I
know whether you know whether I know whether you know whether I know whether
you know whether I know whether you know whether I know whether you know my
number.
Albert: I don’t know your number.
Let whether be Albert’s number.
Cheryl picks (whisper1, whisper2) from the set {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (2, 4), (3, 1), (3, 5)} (this set is known to both Albert and Bernard). Cheryl gives whisper1 to Albert and whisper2 to Bernard.
Cheryl then whispers something to Albert; Bernard observes this but does not hear what Cheryl whispered.
Albert: I don’t know your number.
Bernard: Then you don’t know whether my number is greater than your
number.
Albert: I now know your number.
The answer to this puzzle is six letters long. Cheryl gives Albert the first 3 letters of the answer and Bernard the last 3 letters of the answer. Albert and Bernard are not aware they are in a puzzle hunt, so they believe the answer can be any string of six letters (but as is customary, the answer is indeed an English word or phrase).
Albert: I don’t know if the answer contains exactly
product vowels.
Bernard: I don’t know if the answer contains exactly
product vowels.
Albert: I don’t know if the answer contains
state as a substring.
Bernard: I don’t know if the answer contains
state as a substring.
Albert: I don’t know if the sum of the
whisper1th and
sumth letters (where A = 1, B = 2, …) is
at least birthmonth.
Bernard: I don’t know if the sum of the
whisper1th and
sumth letters (where A = 1, B = 2, …) is
at least birthday.
Albert: I don’t know if the scrabble score of the answer is equal to
edges.
Bernard: I don’t know if the scrabble score of the answer is equal to
whether.
Albert: I don’t know if the set of letters in the answer contains
nonogram consecutive letters.
Bernard: I don’t know if the set of letters in the answer contains
nonogram consecutive letters.
Albert: I don’t know if the whisper2th letter, the
div1th letter, and the
div2th letter of the answer form a
common English word when concatenated.
Bernard: I don’t know if the d1th letter, the
d2th letter, and the
d3th letter of the answer form a
common English word when concatenated.
Albert: I don’t know if the product of all the letters (where A = 1, B = 2,
…) in the answer is divisible by
cell.
Cheryl: Oh, I forgot to tell you this earlier, but all the letters in the
answer are distinct.
Bernard: I know the answer to this puzzle.
Albert: I know the answer to this puzzle.