Food Court
The two food courts, each with ten restaurants, are struggling. We brought in consultants to assess the situation, but can’t make heads or tails of their report!
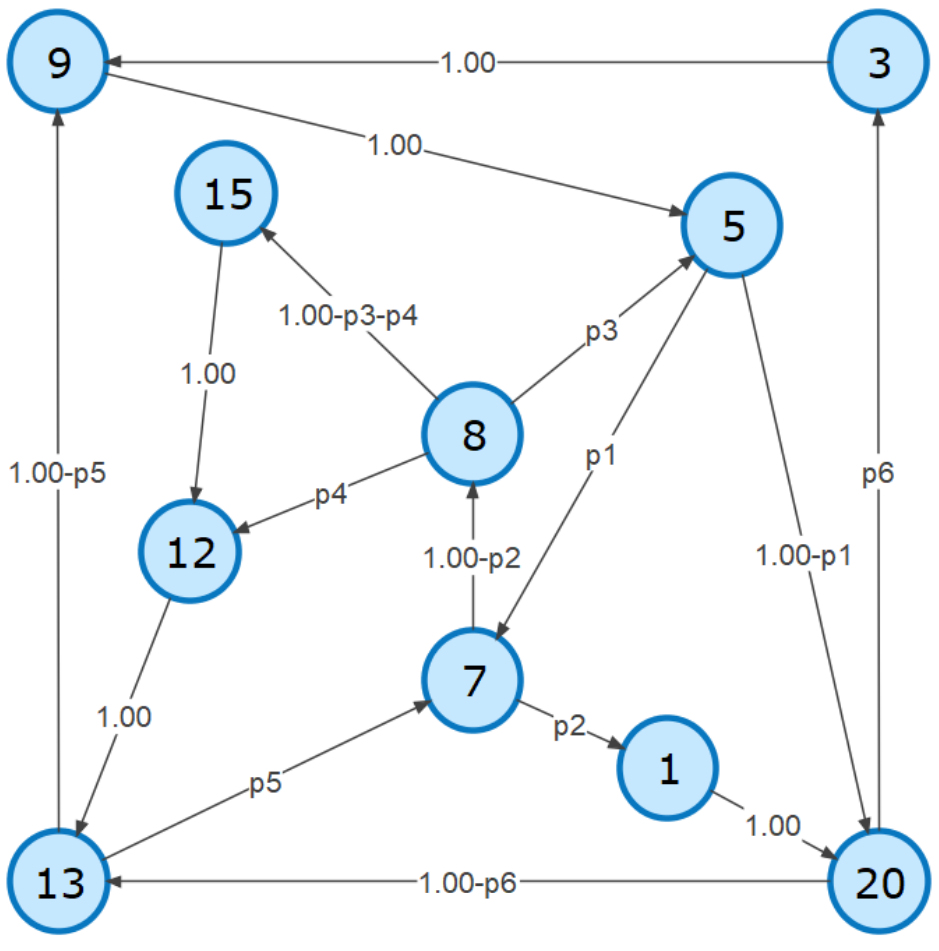
p1. Alice received 15 votes for best chili in a landslide victory over Bob, who only got 4 votes. The ballots were counted one-by-one in random order. What is the probability that Alice was always strictly ahead of Bob in votes during the counting process?
p2. To decide who gets to manage the cash register, Alice, Bob, and Carol take turns flipping a coin, in alphabetical order (Alice→ Bob→ Carol→ Alice, etc.). The first to flip heads wins. What is the probability that Carol wins?
p3. Alice picks pizza toppings by spinning a bottle. The bottle can point to one of six different toppings, spaced evenly around the bottle. Suppose four pizza toppings are chosen in this way. What is the probability that (at least) one topping is chosen twice or more?
p4. Alice absentmindedly cut a carrot at some random point along its length, yielding two pieces. What is the probability that the longer piece is at least 8 times the length of the shorter piece?
p5. To pass the time during a lunch break, Alice plays a (fair) game of Three-Card Monte with Bob and loses track of the target card, and so chooses a card at random. Bob reveals to Alice that one of the other two cards is NOT the target, and gives Alice the opportunity to switch to the remaining card instead. Suppose Bob would’ve made such an offer regardless of Alice’s initial choice. What is the probability Alice wins by switching?
p6. Alice, Bob, and Carol draw straws to decide which one of them has to write the new menu. They have, respectively, a 1/10, 2/5, and 3/5 chance of making typos on a menu. If the menu ends up with typos, what is the (conditional) probability that Alice wrote it?
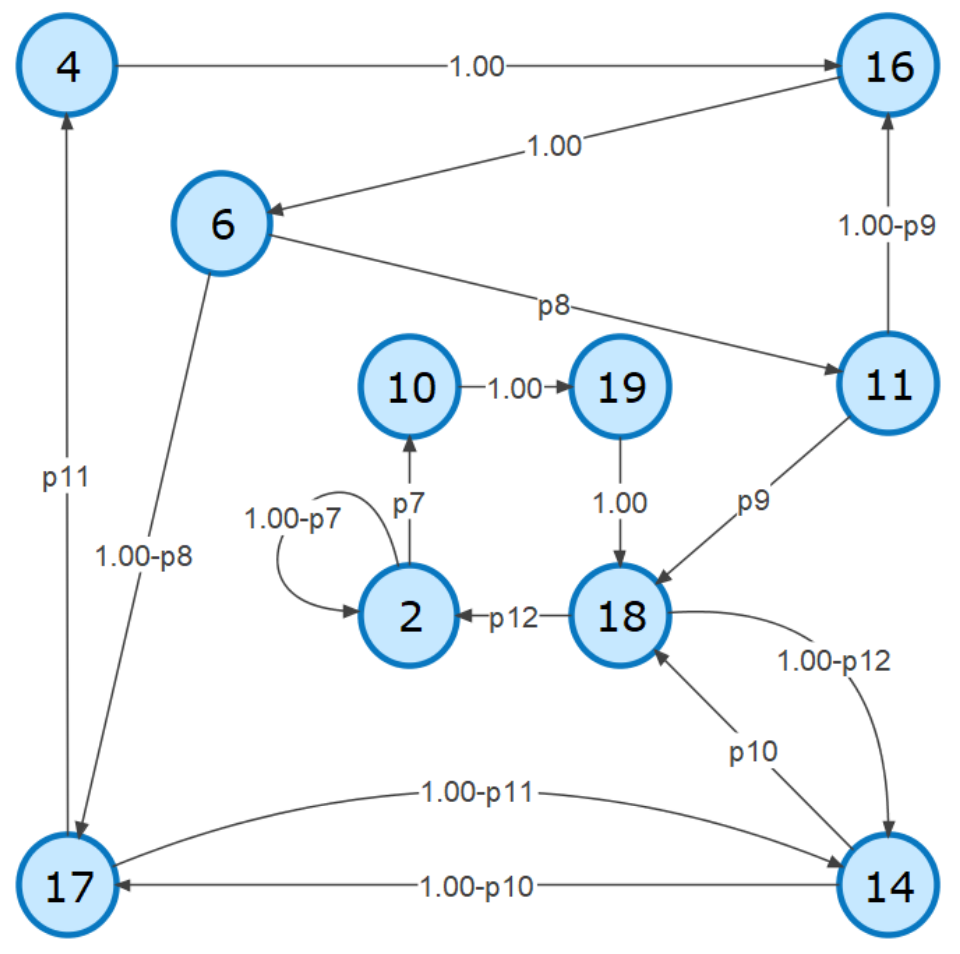
p7. Alice noticed that it takes, on average, 1 minute to serve a customer; moreover, customers arrive, on average, every 2 minutes. Alice can only serve one customer at a time, and so additional customers wait in line. Suppose that both the time between customer arrivals as well as the service time are exponentially distributed. What is the probability that (at a randomly selected point in time) there are exactly 2 customers waiting in line and/or being served?
p8. Alice got 16 coins from tips, and Bob got 3. They decide to play the following game. Each player chooses one of their own coins. They flip their coins until one is heads, the other is tails. The person with heads keeps both coins. This is repeated until one player gets all the coins. What is the probability that Alice loses her tips to Bob?
p9. Alice plays rock-paper-scissors with Bob to decide who has to take out the garbage. Bob flips a coin, and, if it is heads Bob throws rock; otherwise if the coin is tails Bob employs some mixed strategy. Alice knows about this coin strategy but not the outcome of the coin flip. Suppose the players are in Nash equilibrium. What is the probability that Alice throws paper?
p10. Alice knows there is exactly one mouse in the food court. On a given day, the mouse can decide: to leave (10% chance), stay (60% chance), or invite an additional mouse friend to stay with them (30% chance). All mice (independently) act in the same manner. What is the probability that (absent outside intervention) the food court will ever be free of mice?
p11. Alice wants to know whether a bag of onions is still fresh. A fresh bag of 7-week-old onions spoils within 2 weeks 19% of the time, and has a 73% chance of spoiling within 3 weeks. Furthermore, a fresh bag of 8-week-old onions has a 30% chance of remaining fresh for at least 2 weeks. What is the probability that a fresh bag of 8-week-old onions will remain fresh for at least 1 week?
p12. Alice has a 40% chance of working a given shift at the food court; Bob has a 30% chance. The chance that either Alice and/or Bob are working a shift is 50%. What is the probability that Alice and Bob are working together?