Domino Maze
by Wei-Hwa Huang
Answer: MAJESTIC PLURAL
The solver is given an original, untouched set of Domino Maze by ThinkFun, along with a custom deck of "Mystery Hunt Challenge Cards".
The cards in the deck seem pretty normal -- there's a challenge on one side of each card, but the challenge's solution is on the back of the card. Setting up the solution reveals that it's a perfectly legitimate solution that follows the rules. So where's the puzzle?
A natural start point is to read the text on the box, which suggests there's a hidden message that can be used to find a "7-letter phrase that's a synonym of the 14-letter answer". But it doesn't tell you how to find the hidden message.
Reading the rest of the text, an astute reader should notice that there seems to be a lot of text dedicated to precisely specifying what counts as repositioning a piece and what doesn't, as well as how to precisely count pieces. This seems like information that isn't actually very useful when solving the challenges normally.
This hints at the first aha for this puzzle -- every single challenge actually has two solutions. Only one of the solutions is printed on the back of the card. The solver has to find the other (unprinted) solution by themselves.
As a possible way to get started, there are several cards (2, 7, 9, 11, 12, 21, 25, 37) that have printed solutions that are identical or near-identical to published cards. By studying the differences between the Mystery Hunt Challenges and the published challenges, one can get a hint towards finding the unprinted solutions.
After finding the other solution, the solver has to figure out how many pieces in the printed solution need to be repositioned to make the other solution. This is where precision in what actually counts as repositioning is important.
The next step is to use that to find the hidden message. This is done by the simple code of 1=A, 2=B, etc., applied to the number of pieces that reposition. For example, challenge card 1 requires 19 pieces repositioned (5 pieces for the upper-level (legs and platform) and 14 pieces on the upper-level) to change the printed solution to the unprinted solution. The 19th letter of the alphabet is S, so challenge card 1 gives the letter S.
Repeating this for all 44 cards gives the message SEARCHFORUNIQUELYSOLVABLEWITHREVERSEDTARGETS. Adding the appropriate spaces, the message becomes "search for uniquely solvable with reversed targets".
This should lead the solver to the second stage of the puzzle, which is to reverse the order of targets in each challenge, and try to solve that challenge again. Determine which challenges have a unique solution.
There are some tricks of varying use and difficulty that can be used to do so. Some challenges (9, 14, 16, 18, 21, 28, 30, 32, 34, 35, 38) have only 1 or fewer targets, which means they are unchanged when the target order is reversed. Some challenges (7, 12, 13, 15, 31, 44) can be solved with fewer pieces than supplied, which means the extra pieces can be placed in lots of potential locations and so the solution can't be unique.
Of the remaining ones, nineteen of the challenges have no solutions—1, 2, 3, 5, 6, 10, 11, 19, 20, 23, 25, 27, 29, 33, 37, 39, 40, 41, 42. This leaves seven challenges that fit the message's criteria of being uniquely solvable: 4, 8, 17, 22, 24, 26, 36.
The next aha is about how to turn those seven challenges into a 7-letter phrase; since their answers are unique, we clearly can't reuse the same trick of counting the number of repositionings between two solutions. The not-so-difficult aha here is to realize that we can just reuse the letters we used to get the 44-letter hidden message. The seven letters in the message that correspond to the seven challenges are ROYALWE.
This is a 7-letter phrase ("Royal We"), which a simple web search should result in the player finding the 14-letter synonymous phrase MAJESTIC PLURAL, which is the answer to the puzzle.
Appendix: Notes and pictures of each individual challenge (right-click and open in new tab/window to see at higher resolution)
| Challenge | Solutions (mouseover or touch for the Unprinted solution, where pieces on the lower-level are in purple) | Letter = Reposition Count; Solving Notes | Solution count when Reversed; Solving Notes | Image of Reversed Solution (if applicable) | |
|---|---|---|---|---|---|
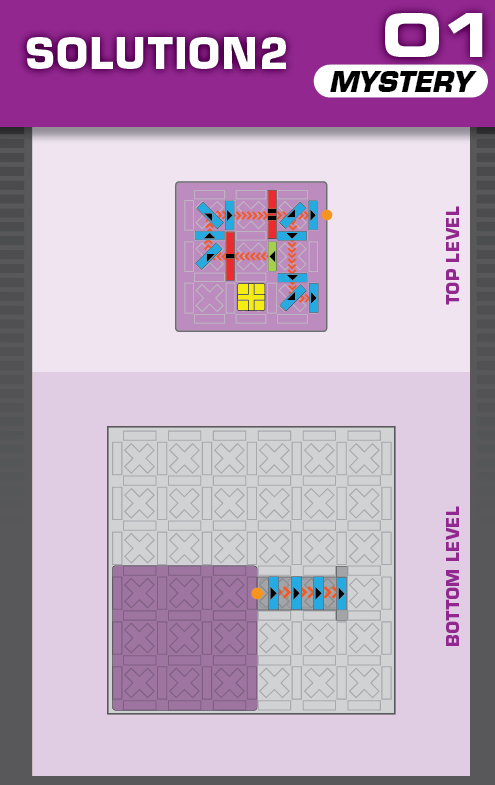
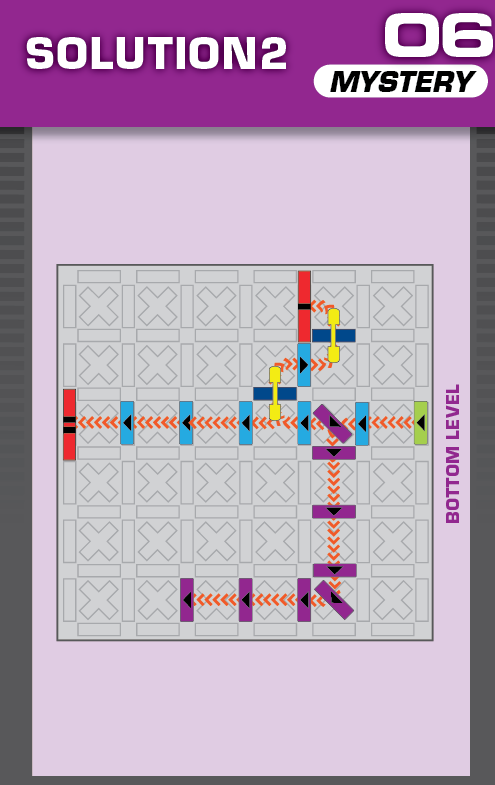
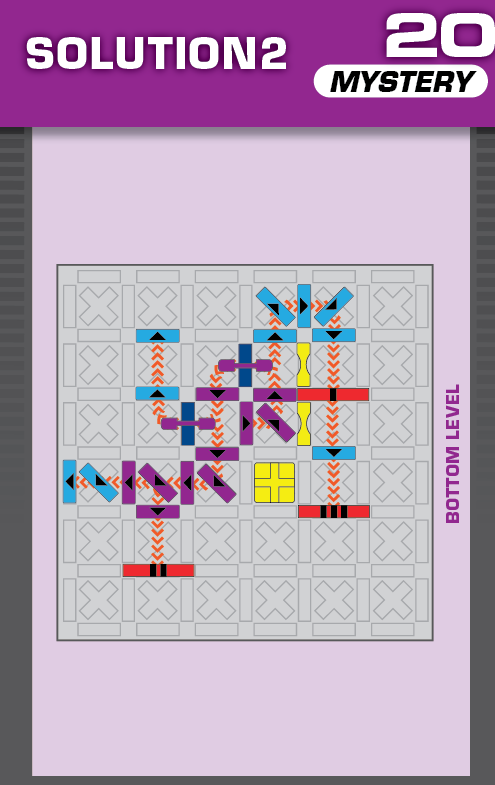
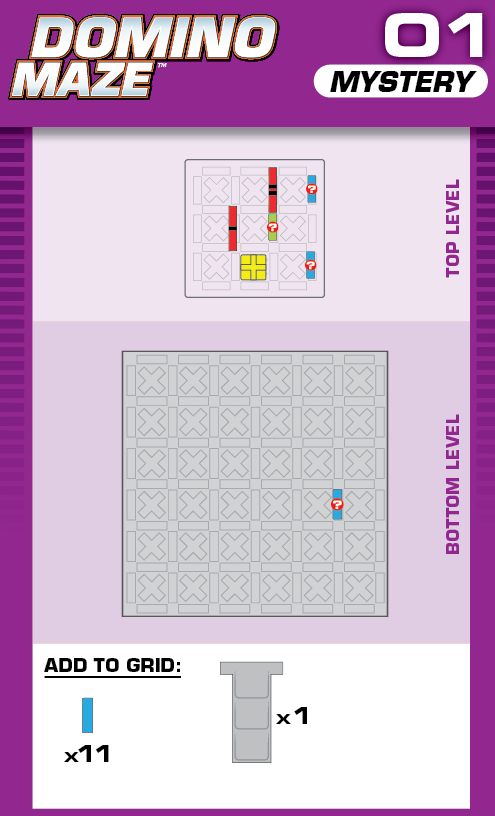 | 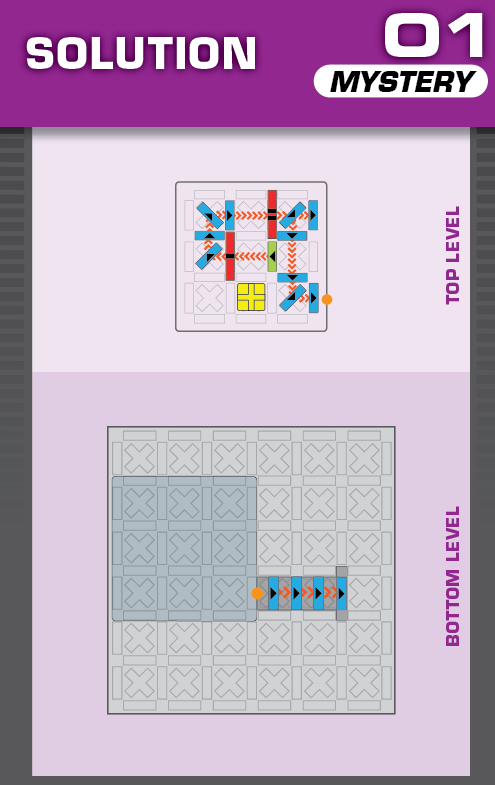 |
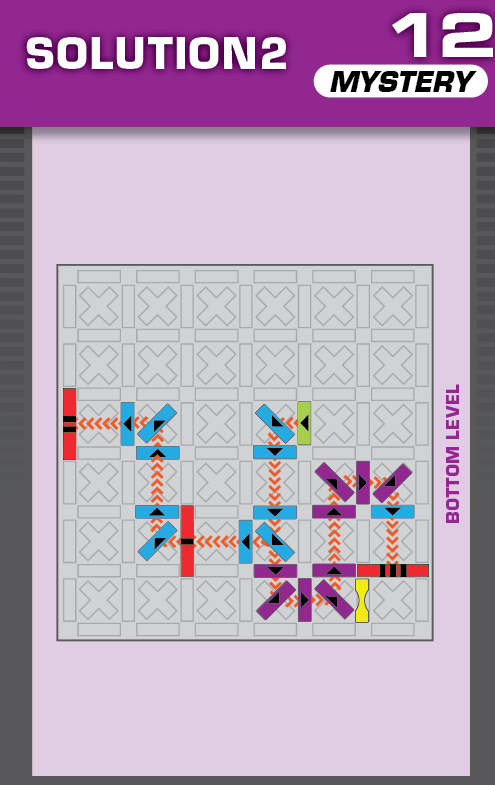
S = 19 | (no solutions) | ||
| The first puzzle is intended to be easy; just moving the top level two spaces south. | (no solving notes) | ||||
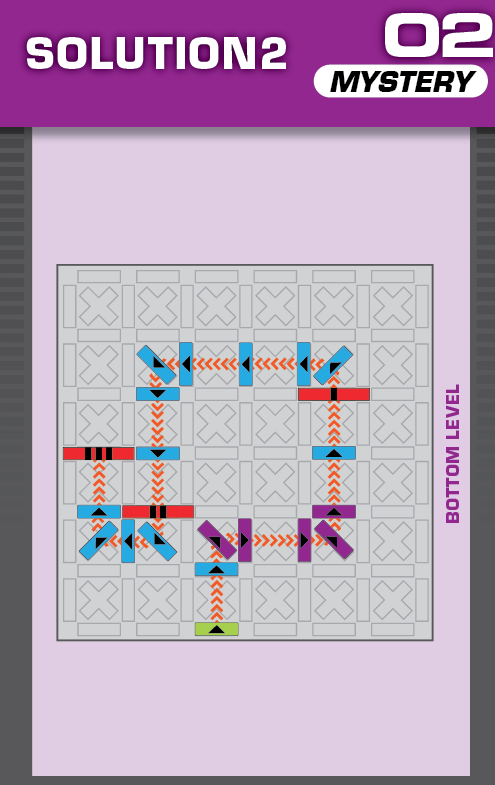
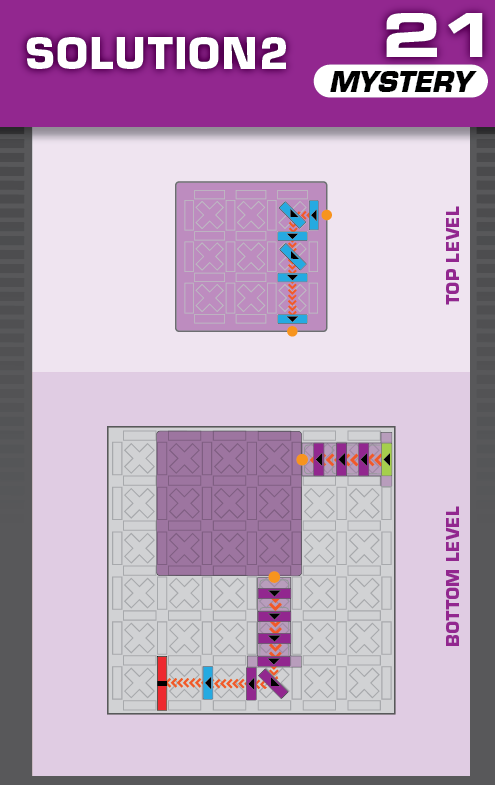
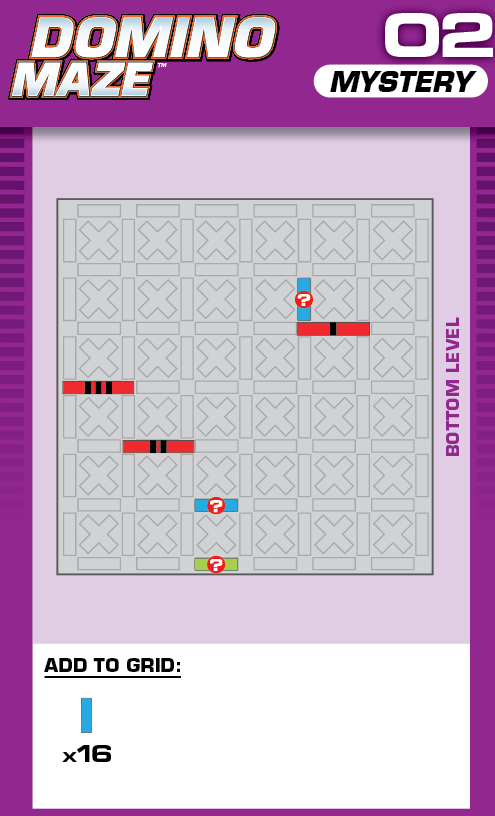 | 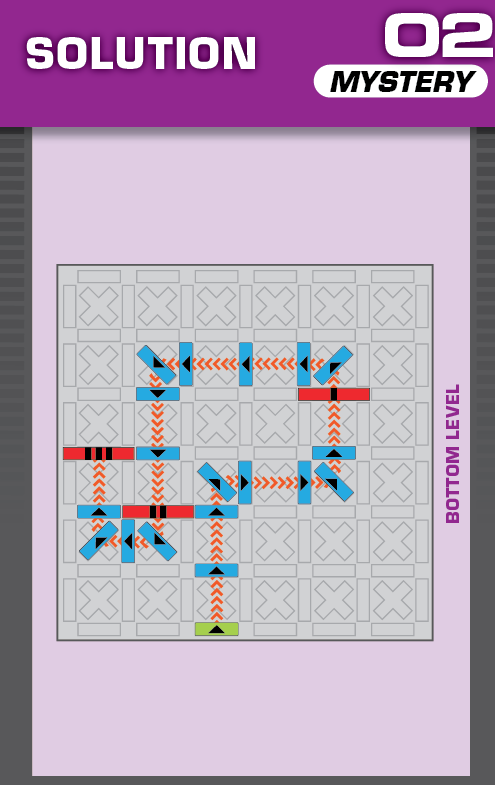 |
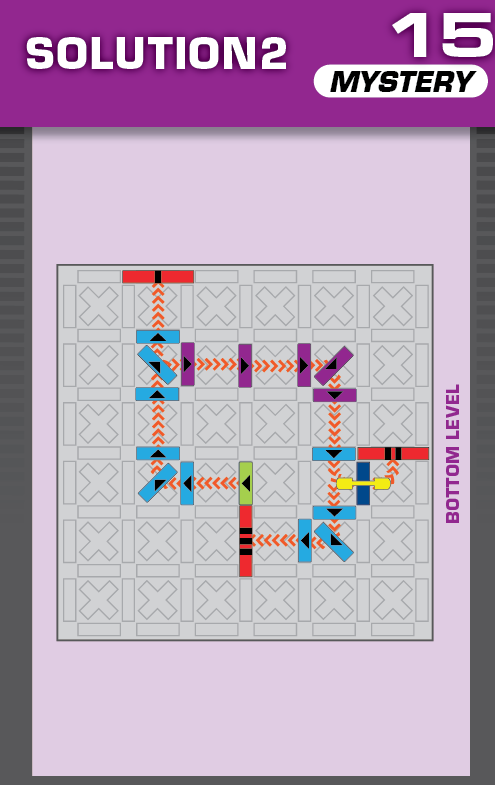
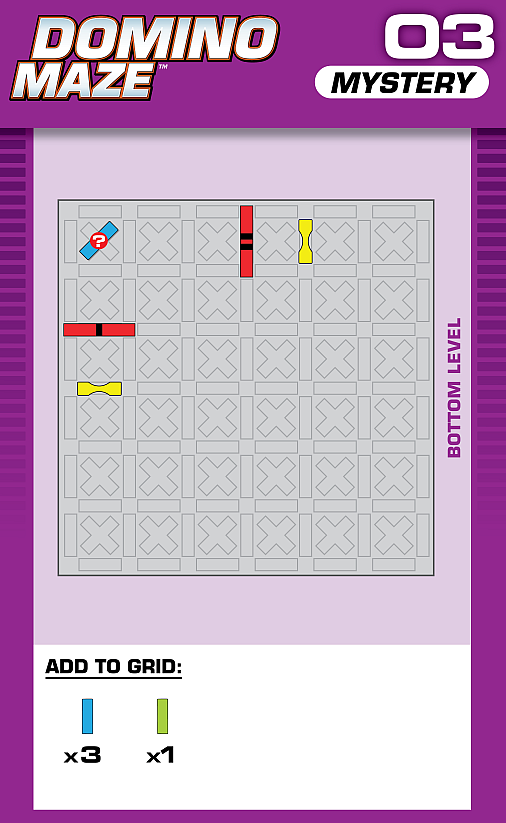
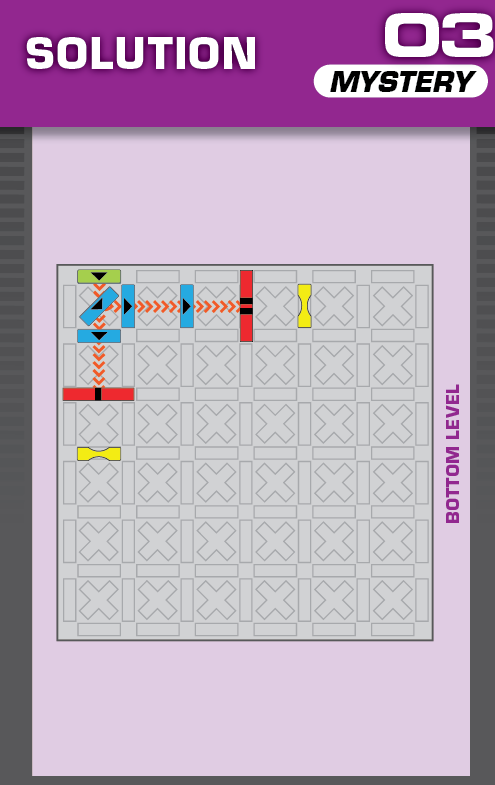
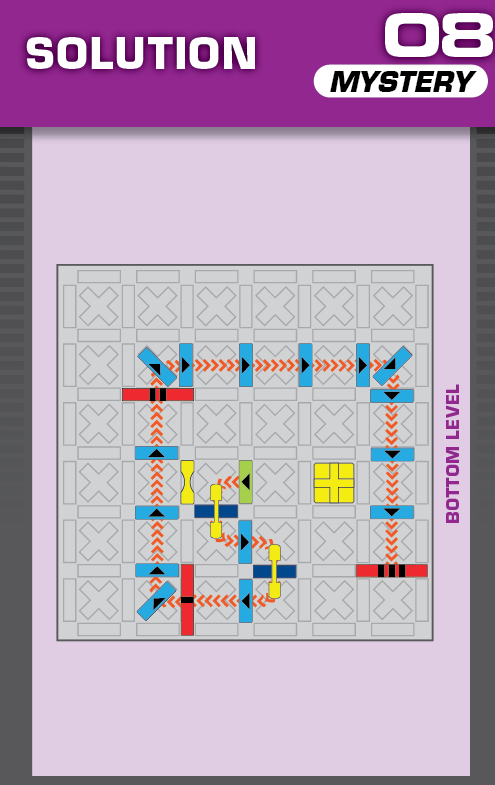
E = 5 | (no solutions) | ||
| This challenge is nearly identical to card 08 in the published deck, but two blockers are missing. The missing blockers should help in determining the unprinted solution. | (no solving notes) | ||||
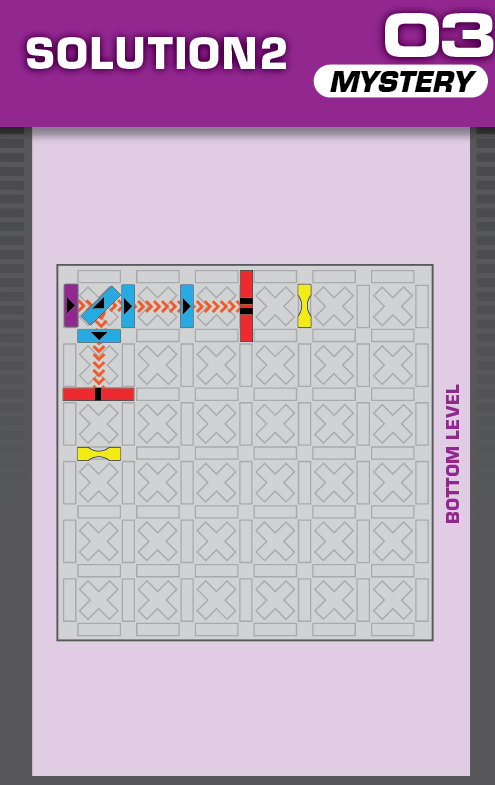
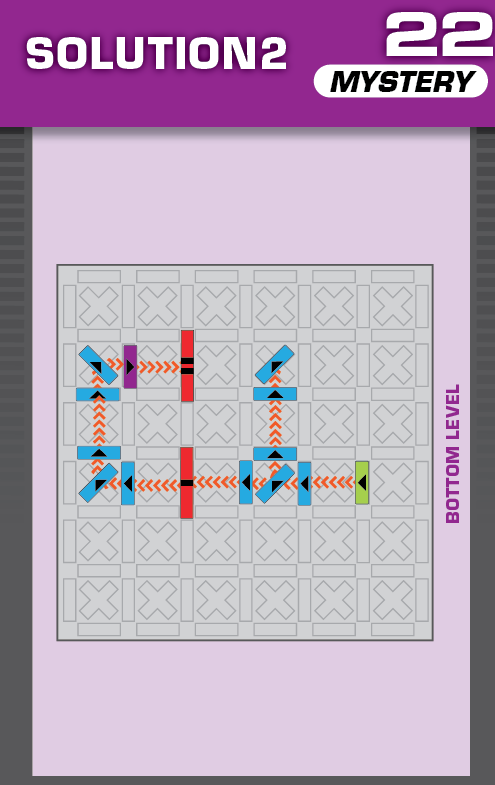
 |  |
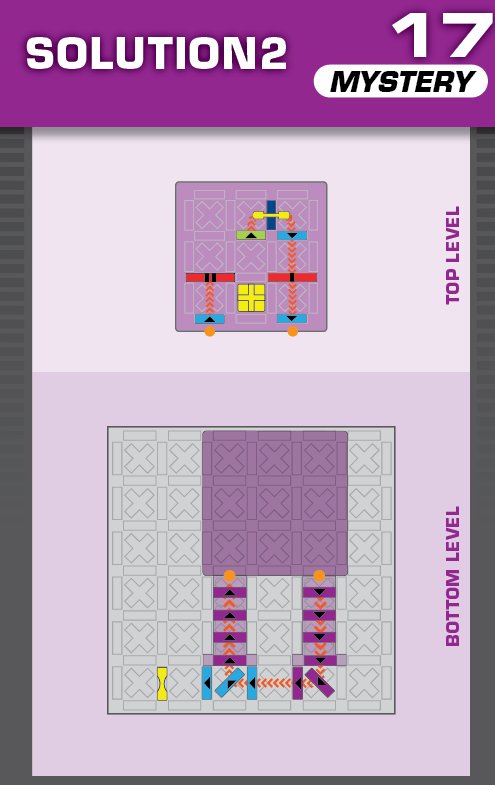
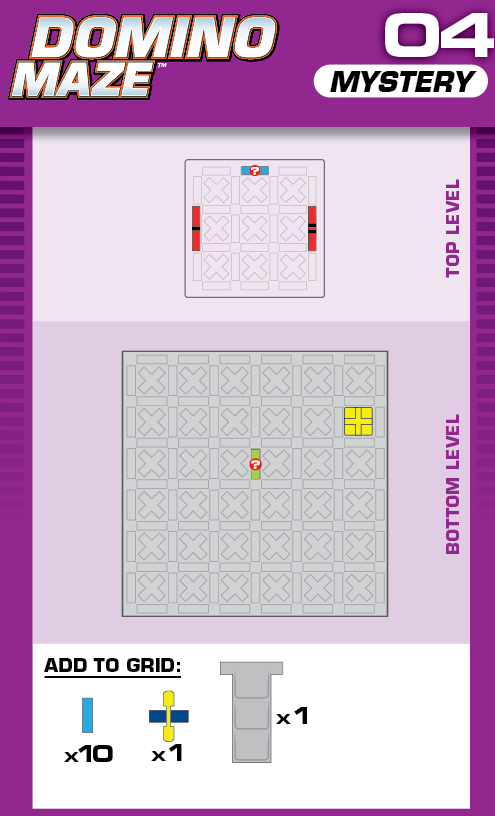
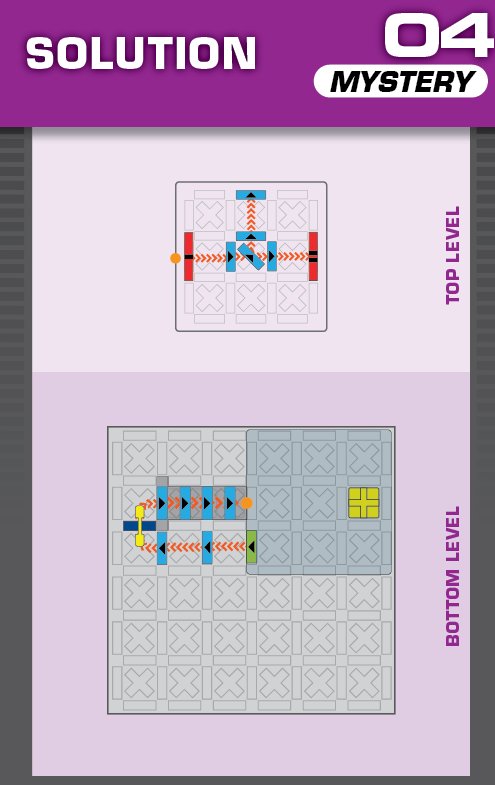
A = 1 | (no solutions) | ||
| The only challenge with no given domino, and it's the only one that moves. | (no solving notes) | ||||
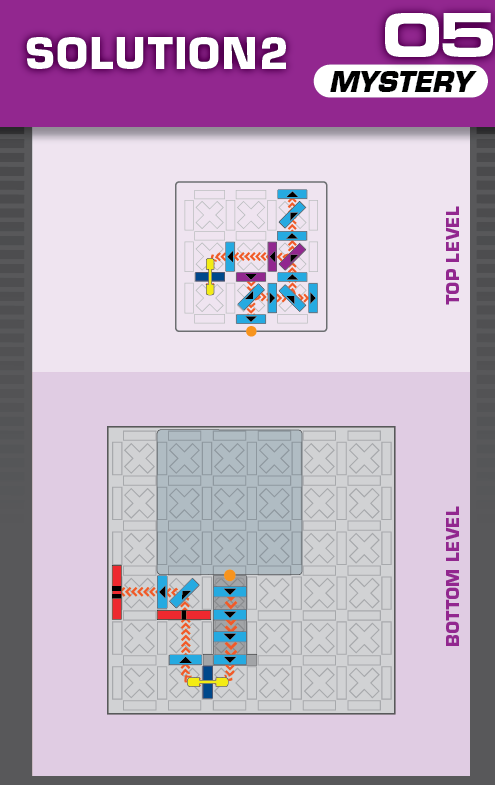
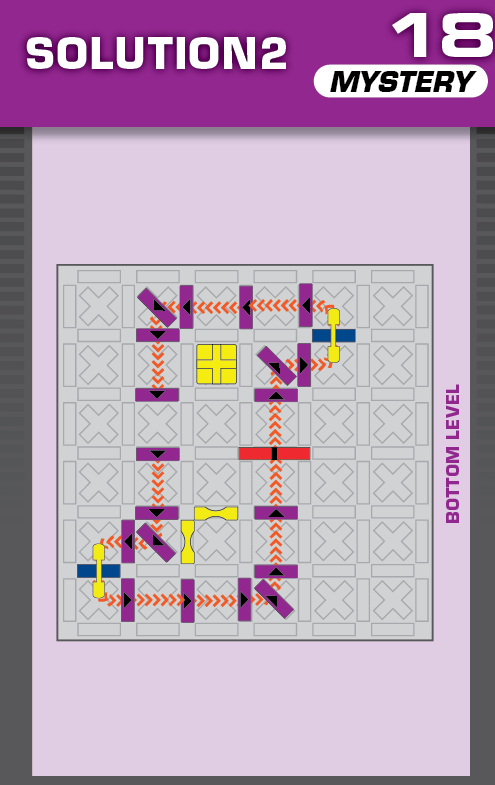
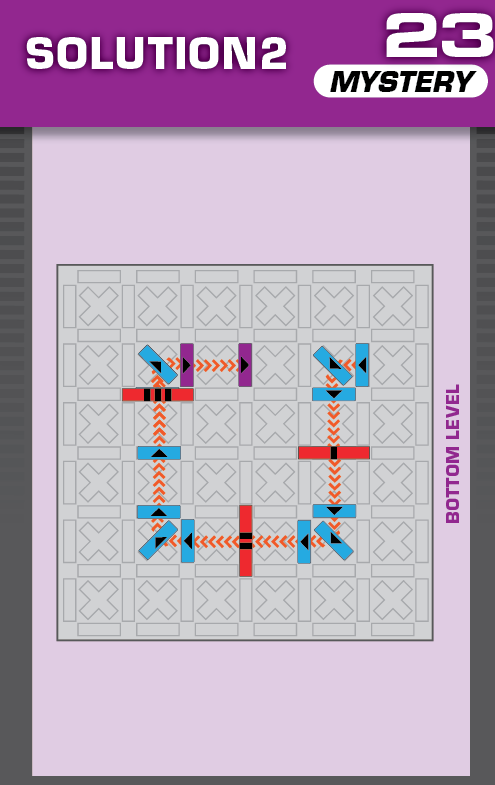
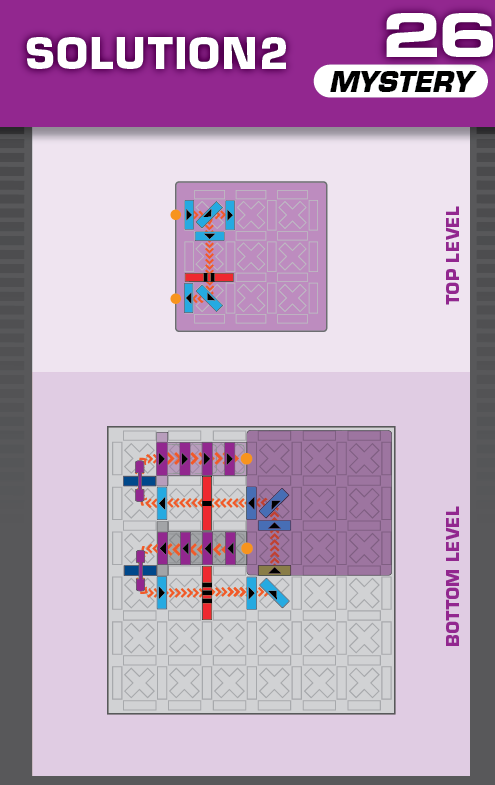
 |  | R = 18 | 1 (unique) |  |
|
| The elevated grid moves south two spaces | This is a left-right reflection of the solution, but now the blocker stops one of the solutions from working. | ||||
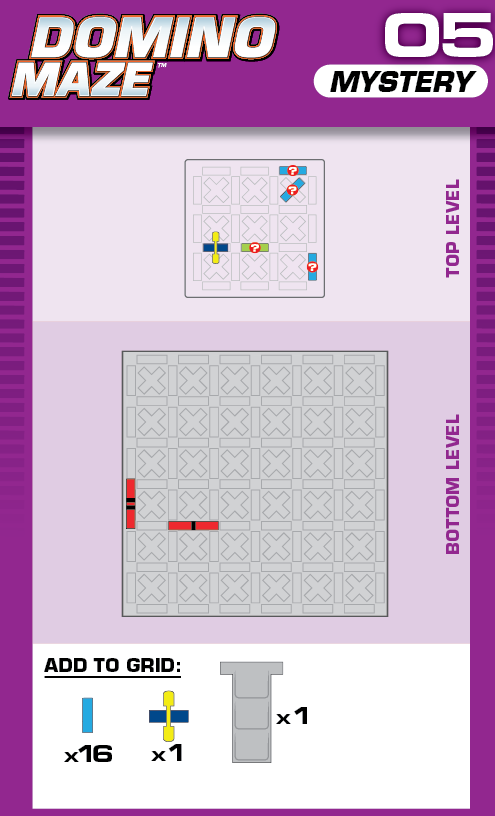 | 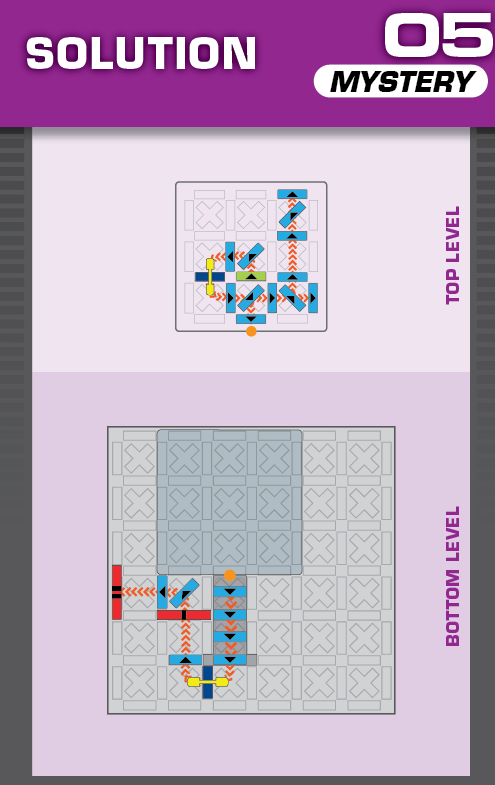 | C = 3 | (no solutions) | ||
| In the unprinted solution, the pivot on the elevated grid is hit but doesn't hit anything else. | Given the number of pieces needed on the top level, there aren't enough left to hit the flags in the other order. | ||||
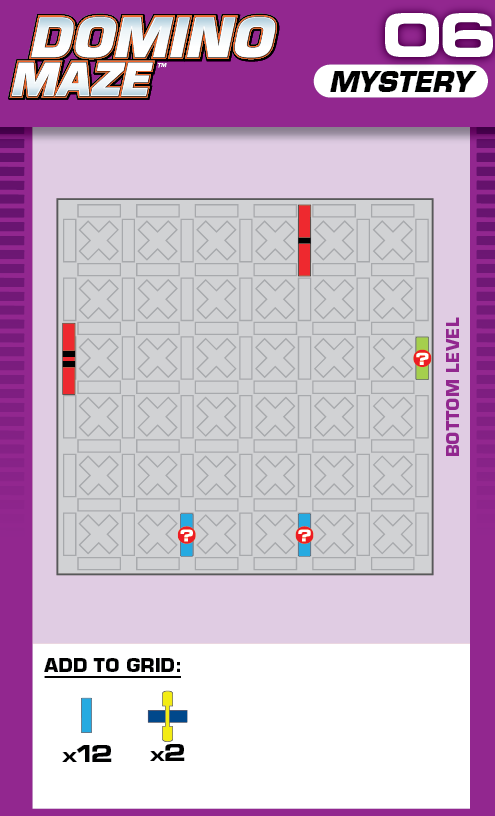 | 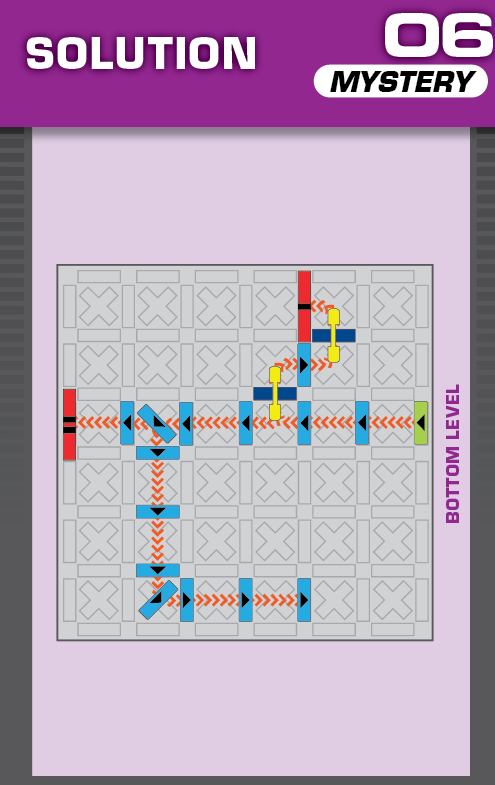 | H = 8 | (no solutions) | ||
| (no solving notes) | (no solving notes) | ||||
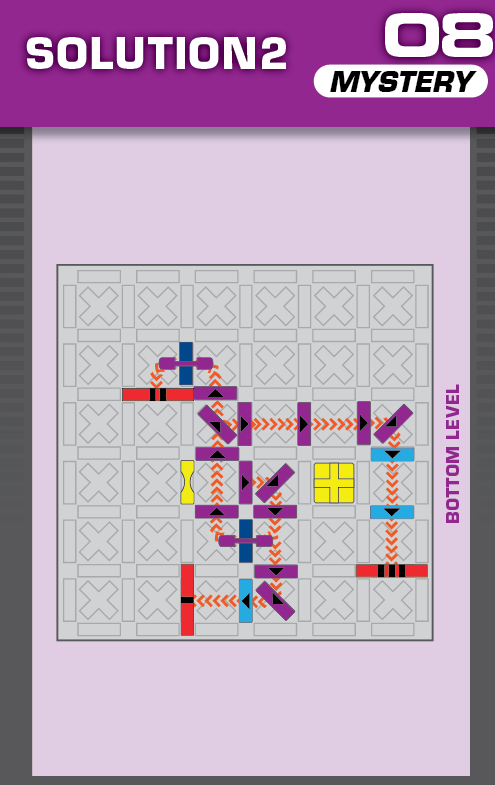
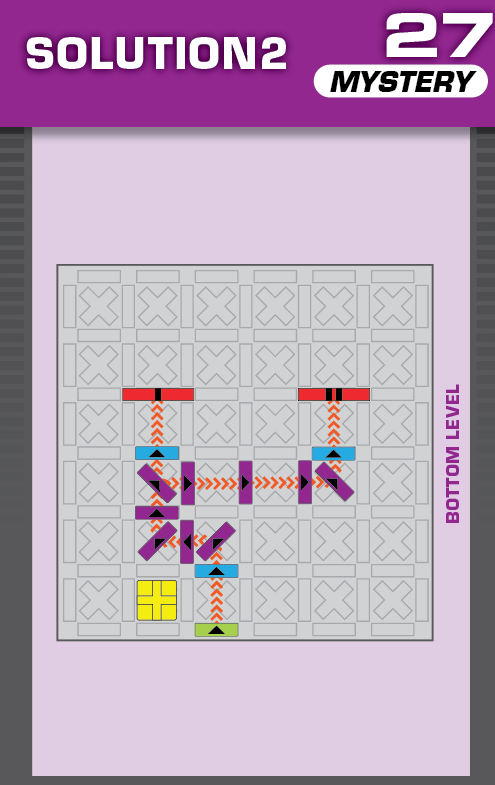
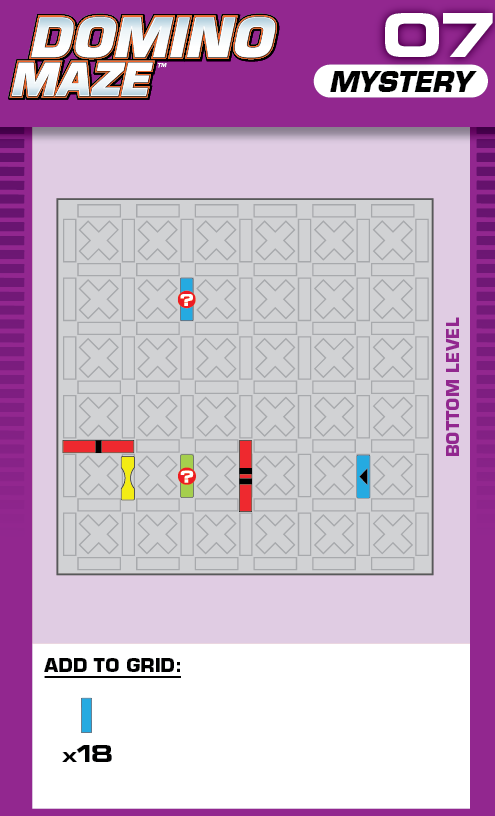 | 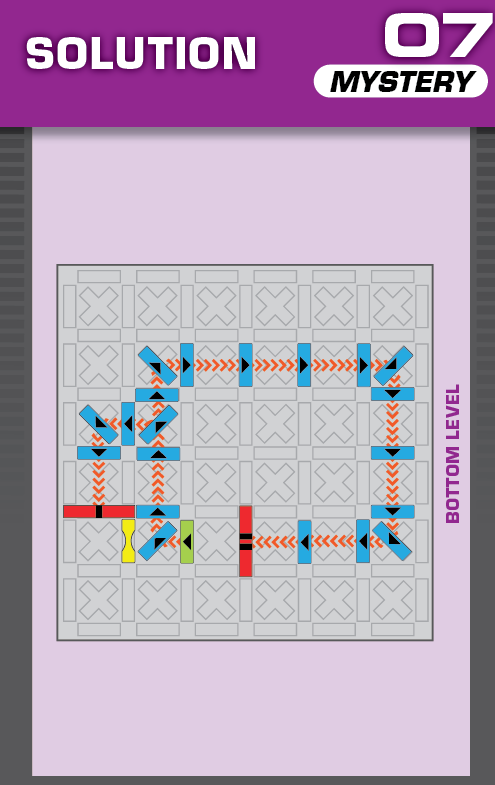 | F = 6 | 253 (2 unneeded dominoes) | 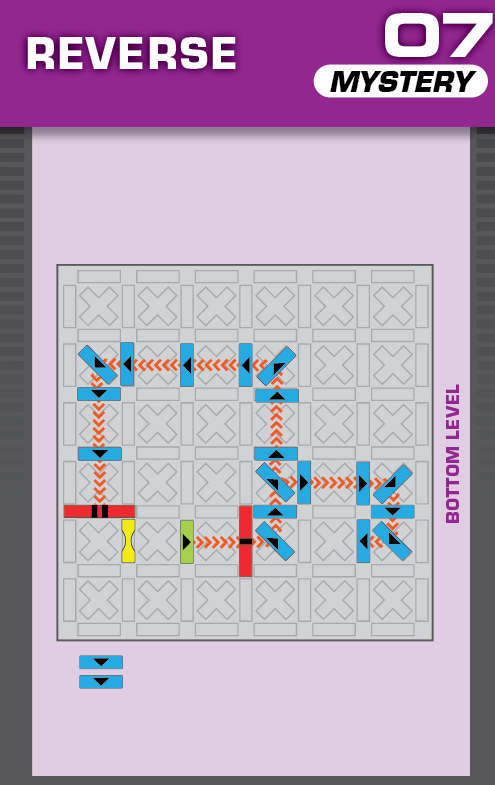 |
|
| This challenge is nearly identical to card 11 in the published deck, but one blocker is missing. The missing blocker should help in determining the unprinted solution. | (no solving notes) | ||||
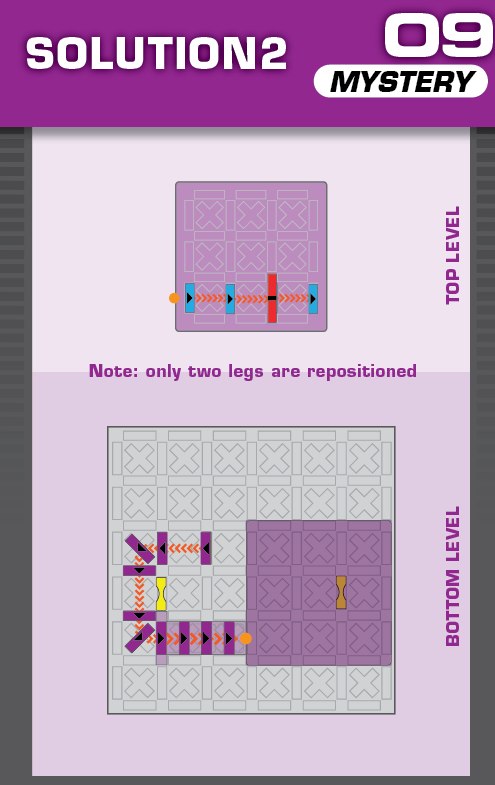
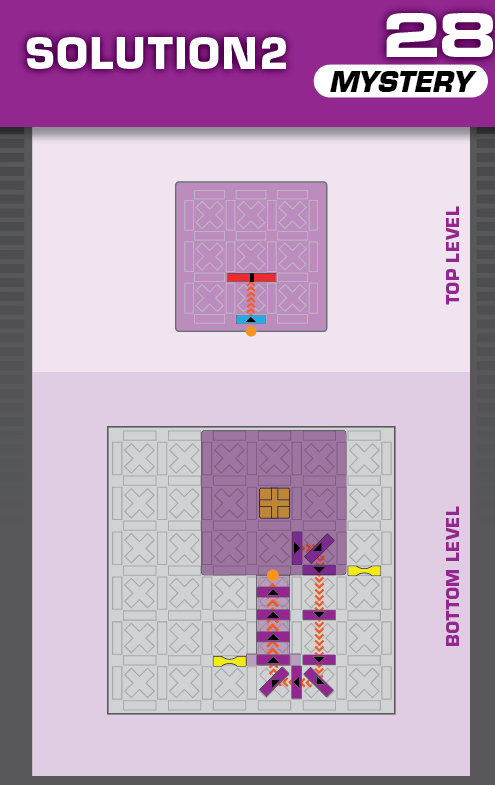
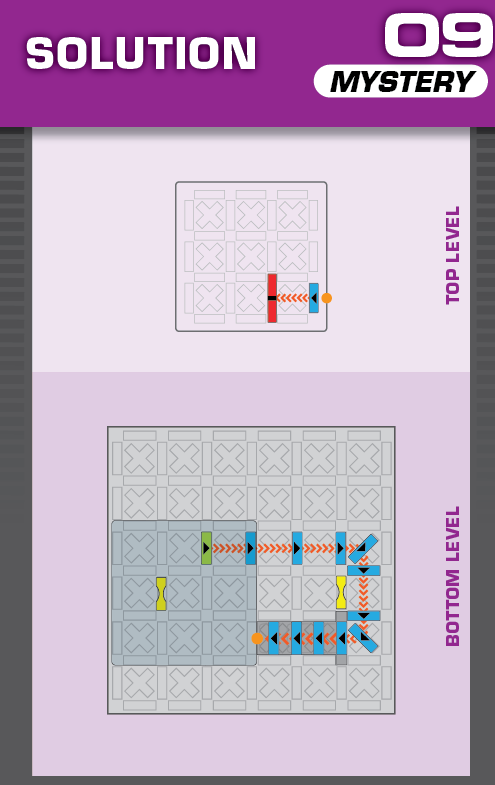
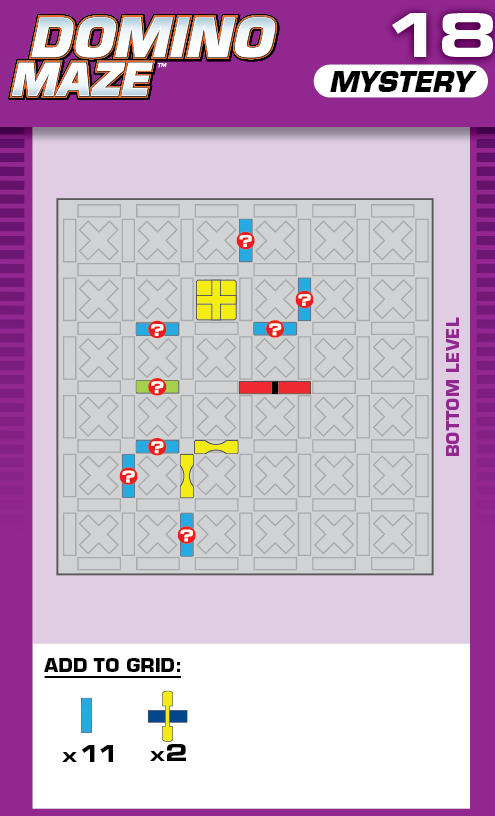
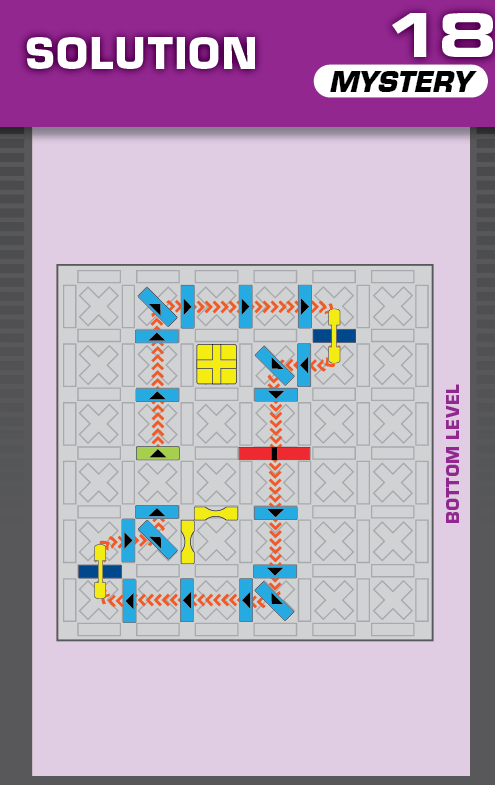
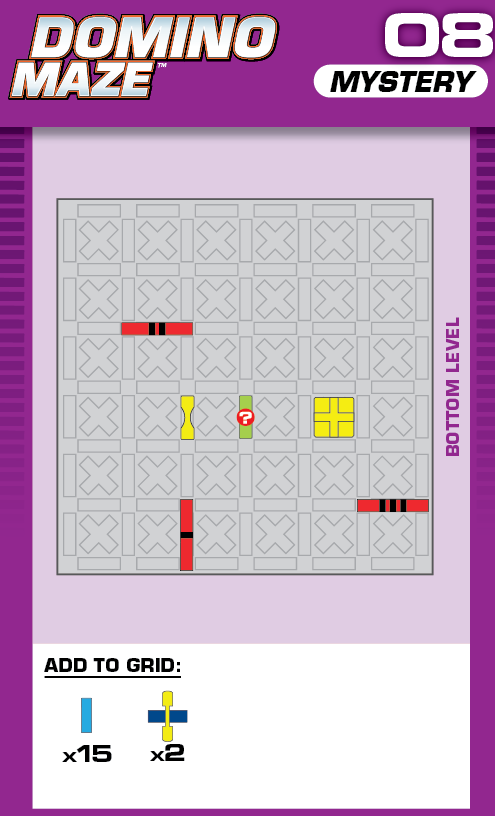 |  | O = 15 | 1 (unique) |  |
|
| This one is legitimately tough; none of the three solutions resemble each other at all. (It was also a pain to construct and make sure there were no other solutions.) | (no solving notes) | ||||
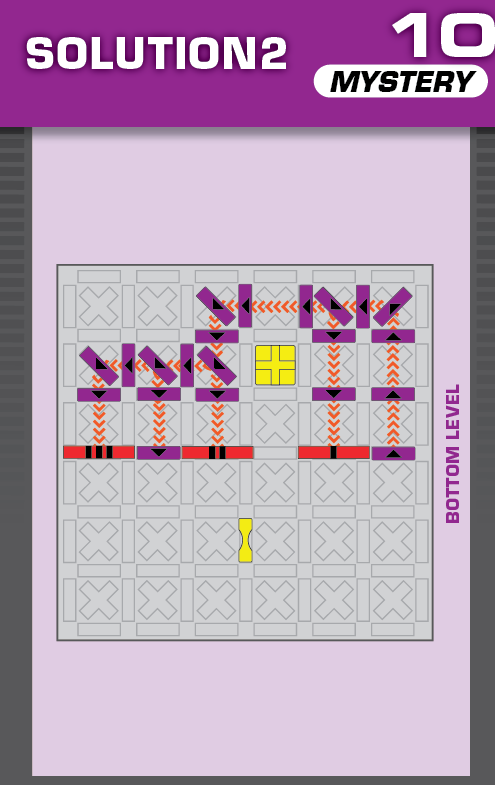
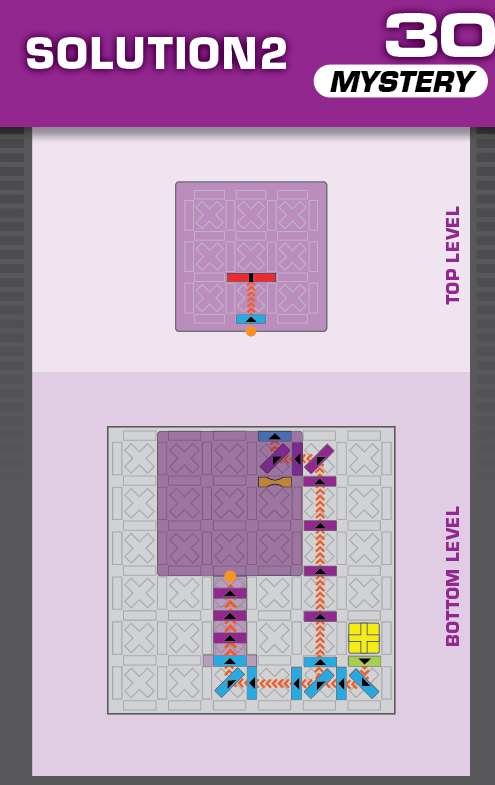
 |  | R = 18 | 2 (unchanged) | ||
| The challenge is similar to card 14 in the published deck, with the same printed solution. | (no solving notes) | ||||
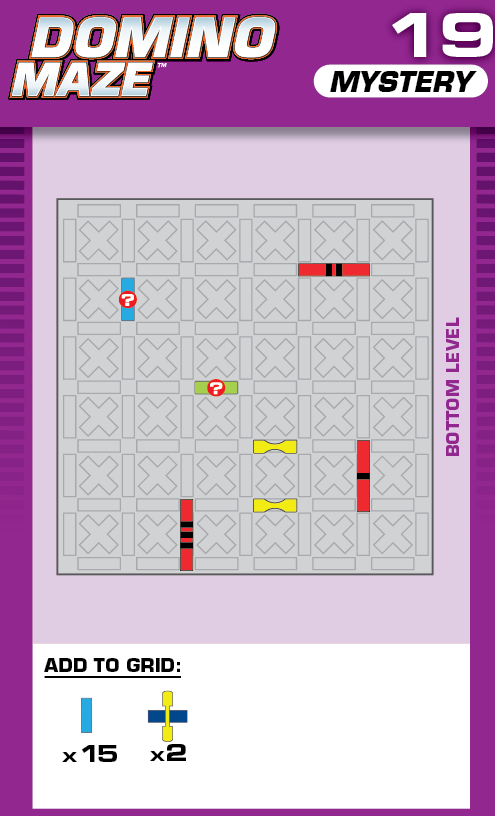
 | 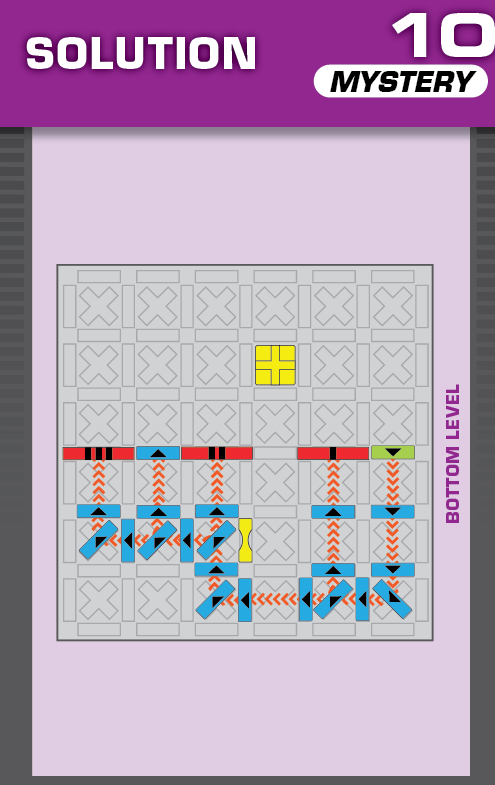 | U = 21 | (no solutions) | ||
| A simple vertical reflection. | (no solving notes) | ||||
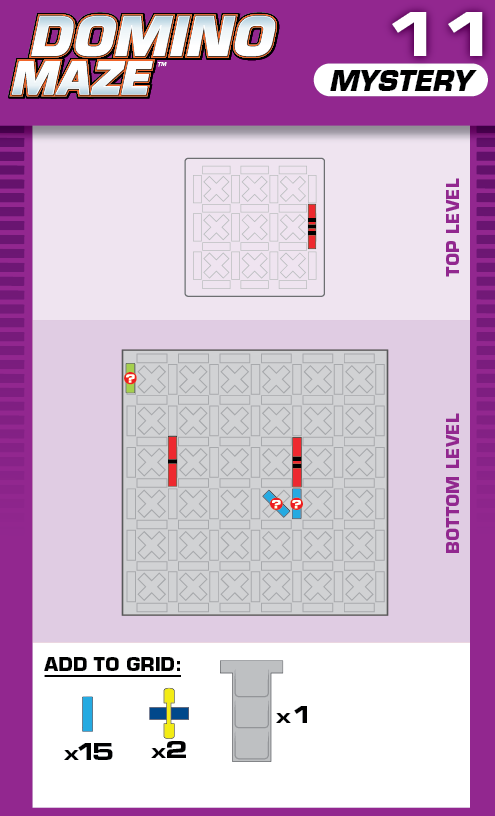 | 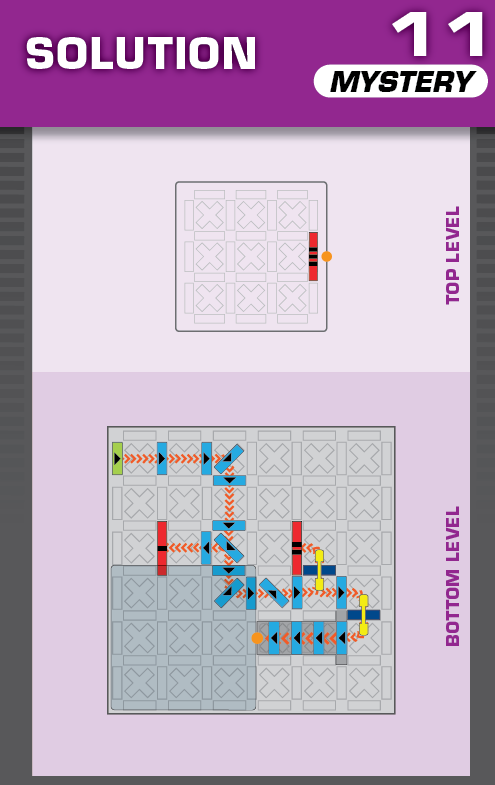 | N = 14 | (no solutions) | ||
| The challenge is similar to card 51 in the published deck, with the same printed solution. | (no solving notes) | ||||
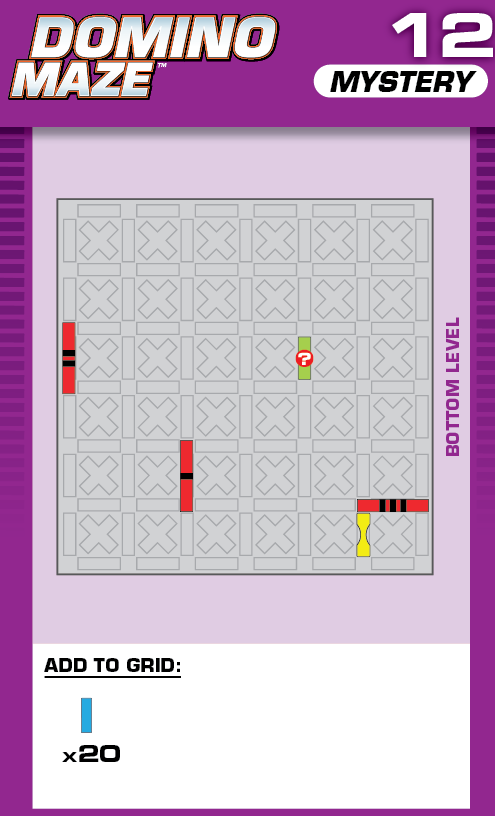 | 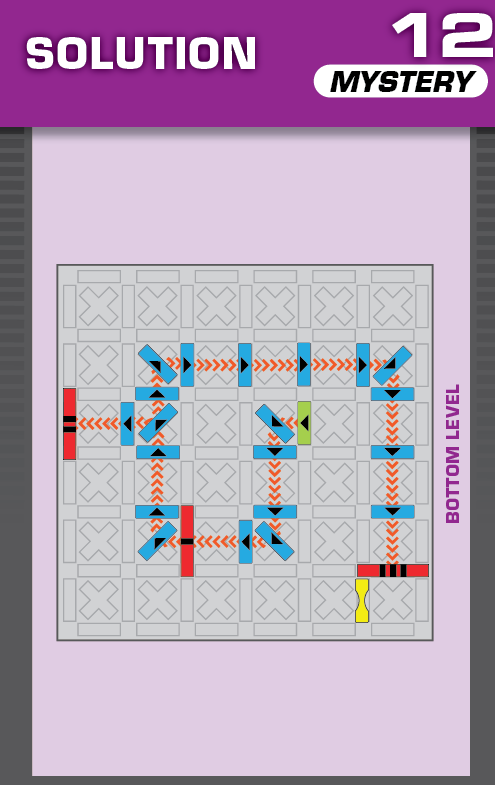 | I = 9 | 226 (2 unneeded dominoes) | 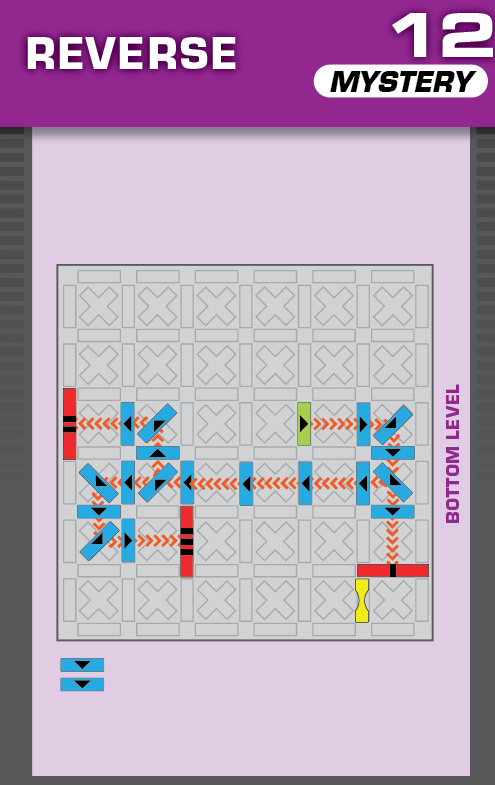 |
|
| This challenge is nearly identical to card 13 in the published deck, but one square blocker has been changed to a wall blocker. The changed blocker should help in determining the unprinted solution. | (no solving notes) | ||||
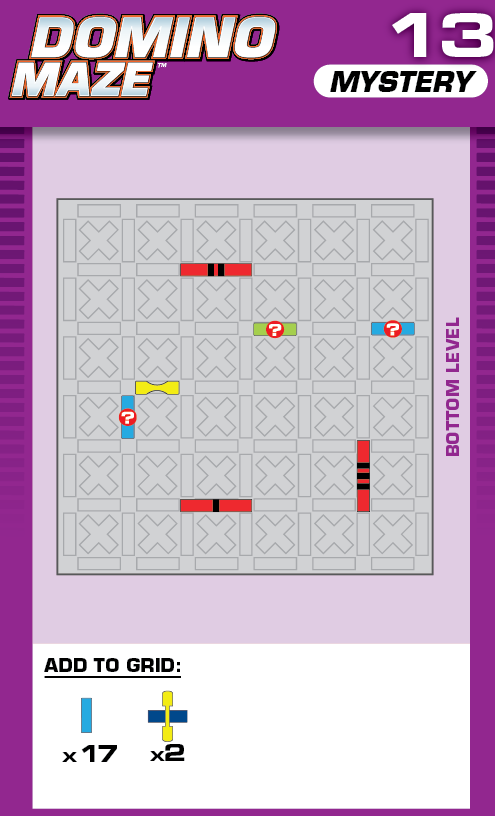 | 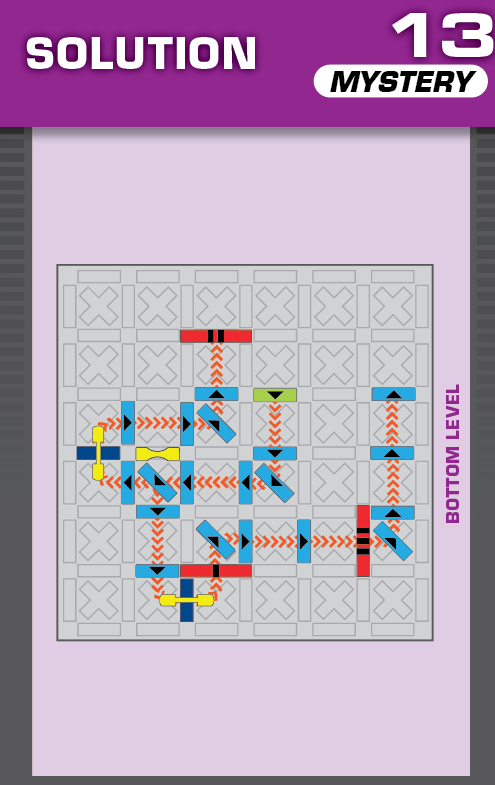 | Q = 17 | 406 (1 unneeded domino and 1 unneeded pivot) |  |
|
| The printed solution is a bit finicky; depending on how the first three dominoes slide after they fall, they may block target 1 from completely raising up. However, this isn't a problem in the unprinted solution. | (no solving notes) | ||||
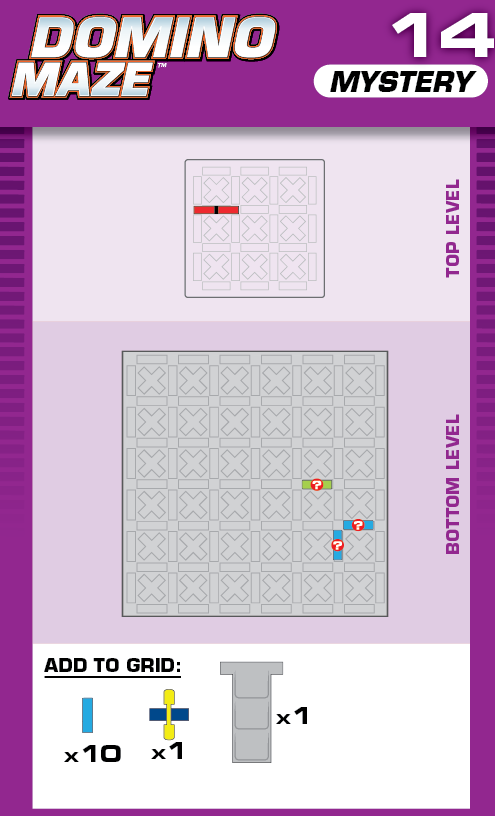 | 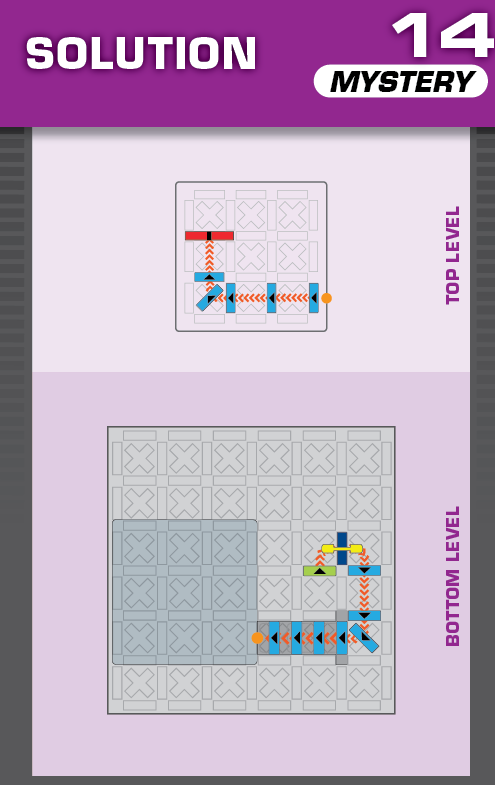 | U = 21 | 2 (unchanged) | ||
| This is nearly identical to challenge 32, with a reflection across the diagonal and one fewer blocker. | (no solving notes) | ||||
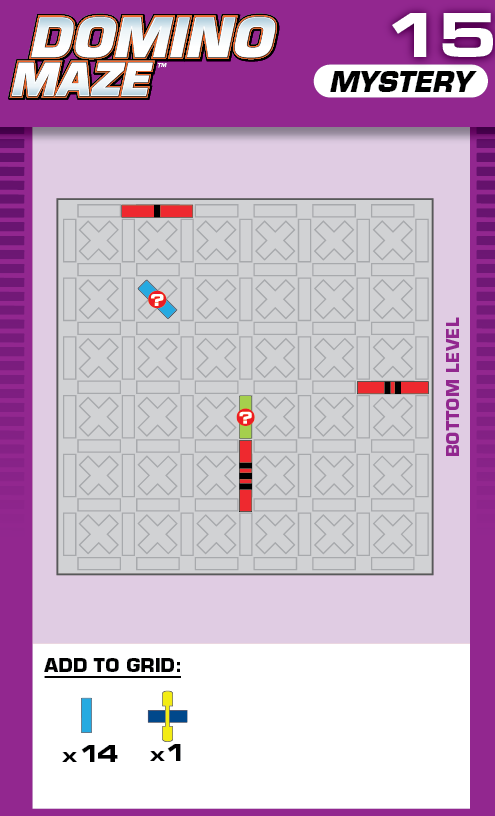 | 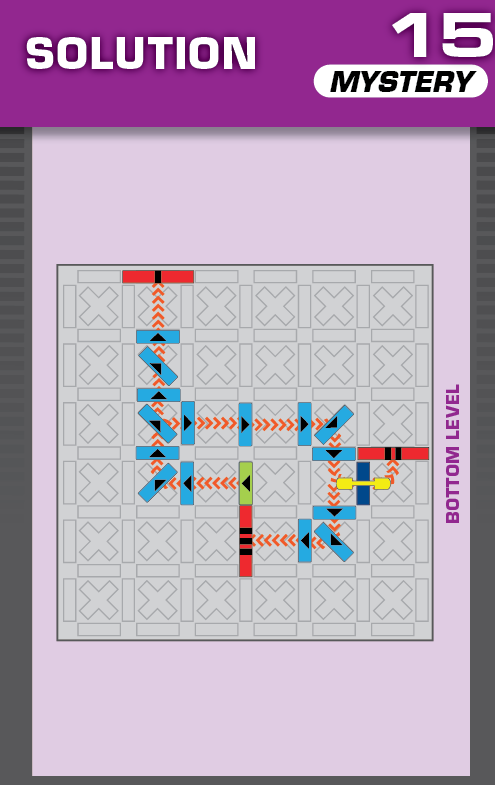 | E = 5 | 644 (2 unneeded dominoes) |  |
|
| (no solving notes) | (no solving notes) | ||||
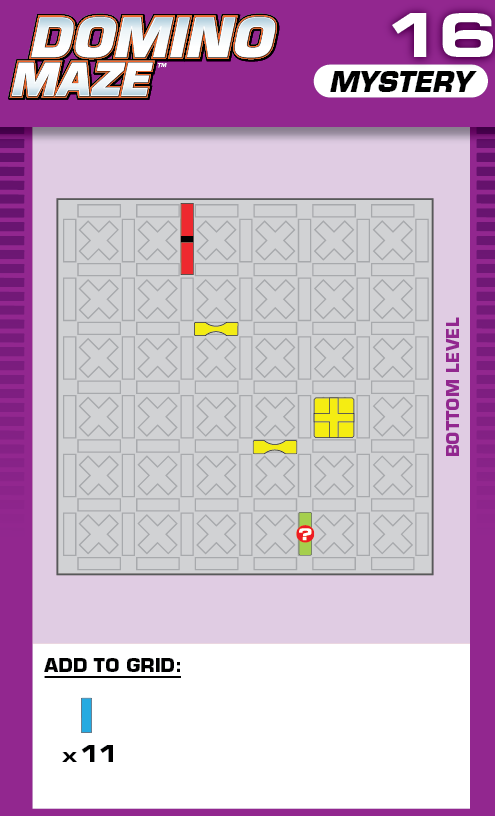 | 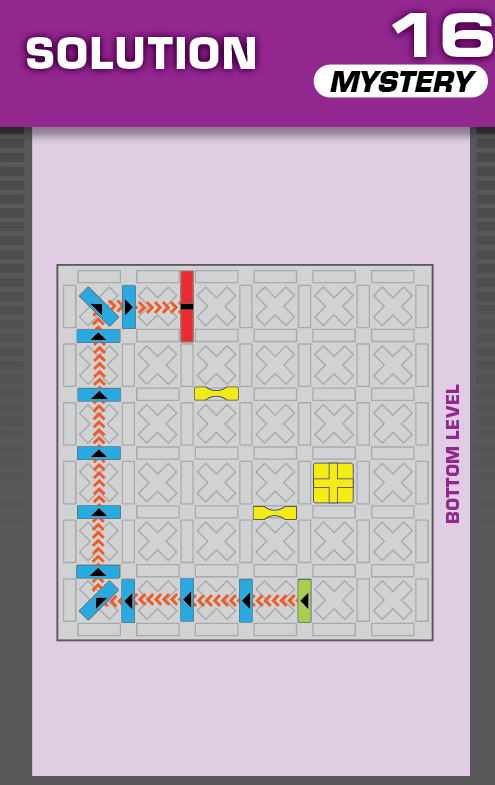 | L = 12 | 2 (unchanged) | ||
| (no solving notes) | (no solving notes) | ||||
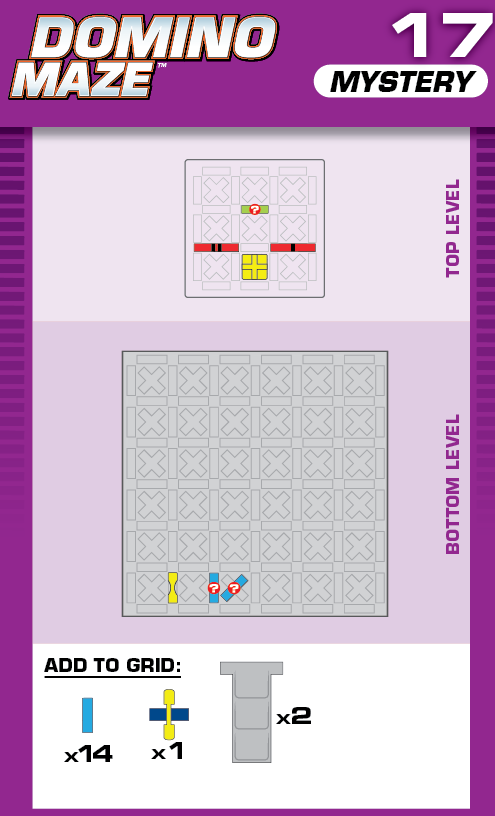 | 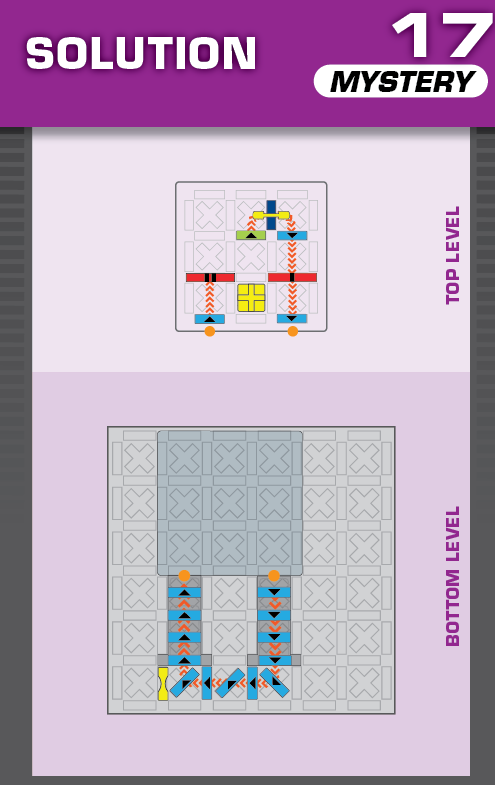 | Y = 25 | 1 (unique) | 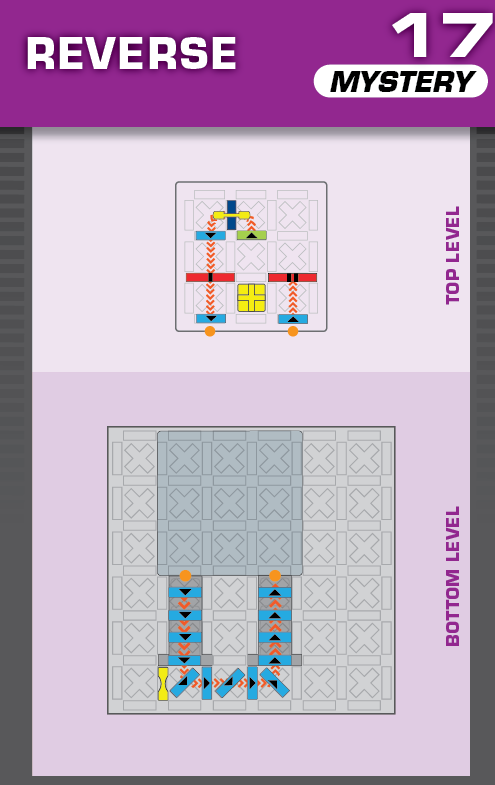 |
|
| (no solving notes) | Note that the diagonal domino stops one of the solutions from working as a reflection. | ||||
 |  | S = 19 | 2 (unchanged) | ||
| Amusingly, all 19 repositions are just rotating a domino in the same location. | (no solving notes) | ||||
 | 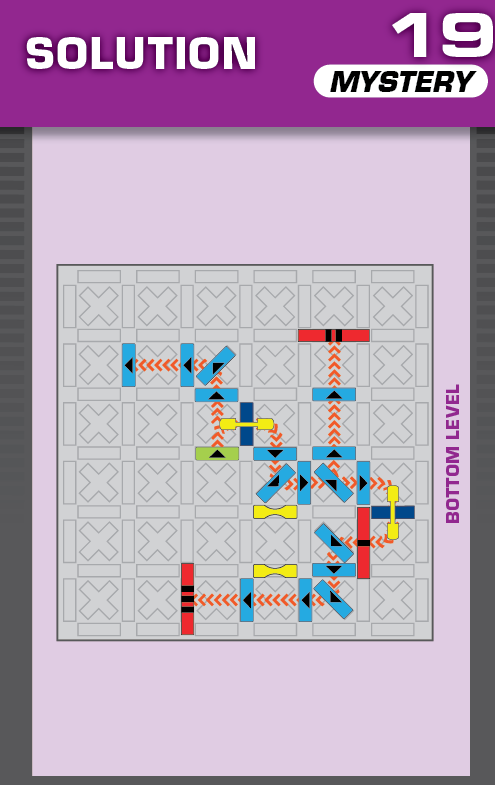 | O = 15 | (no solutions) | ||
| The printed solution has really close timing, where checkpoint 1 gets hit a fraction of a second before checkpoint 2. The unprinted solution is unambiguous. | (no solving notes) | ||||
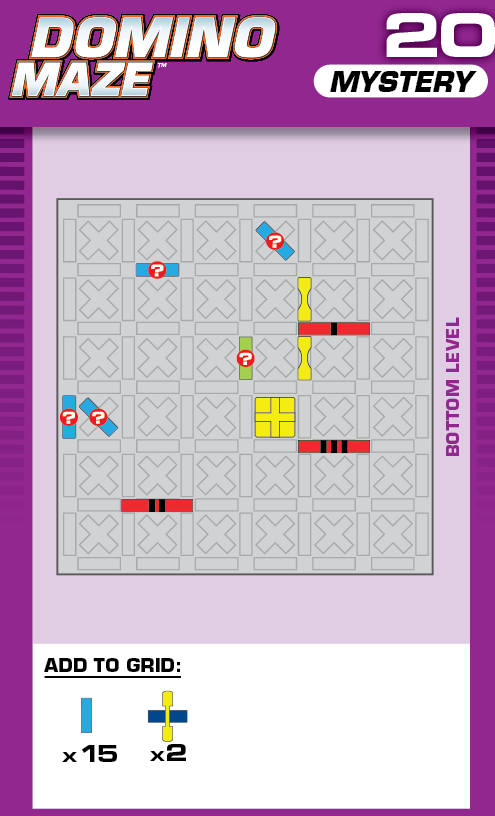 | 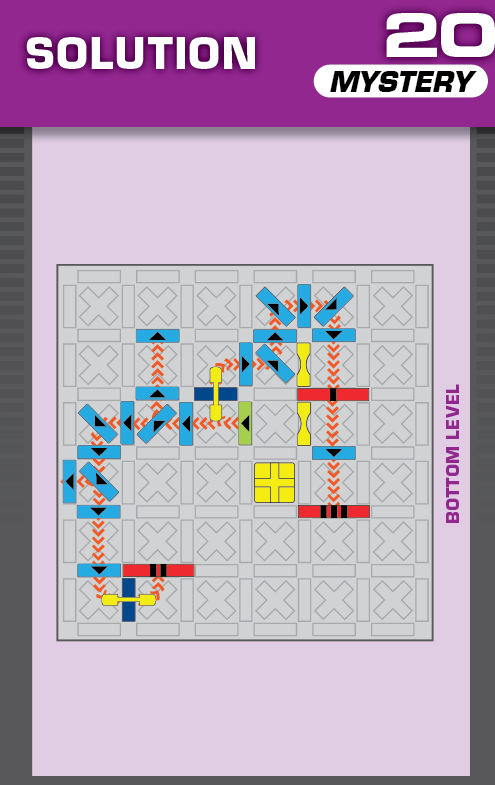 | L = 12 | (no solutions) | ||
| (no solving notes) | (no solving notes) | ||||
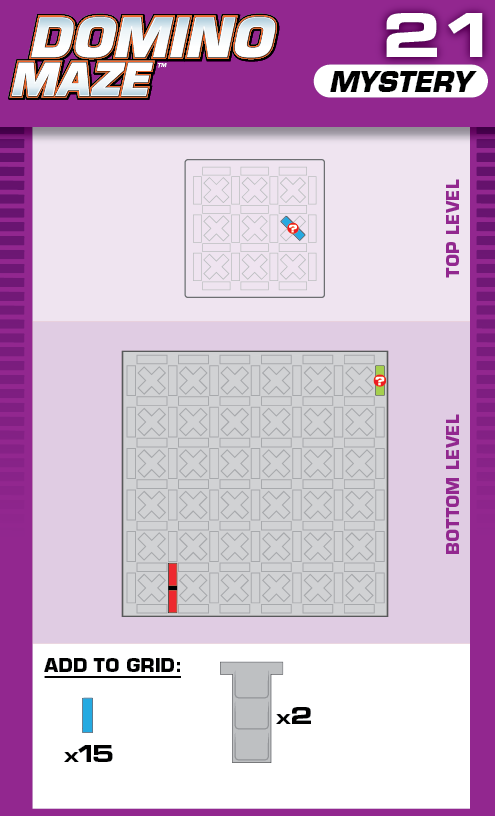 | 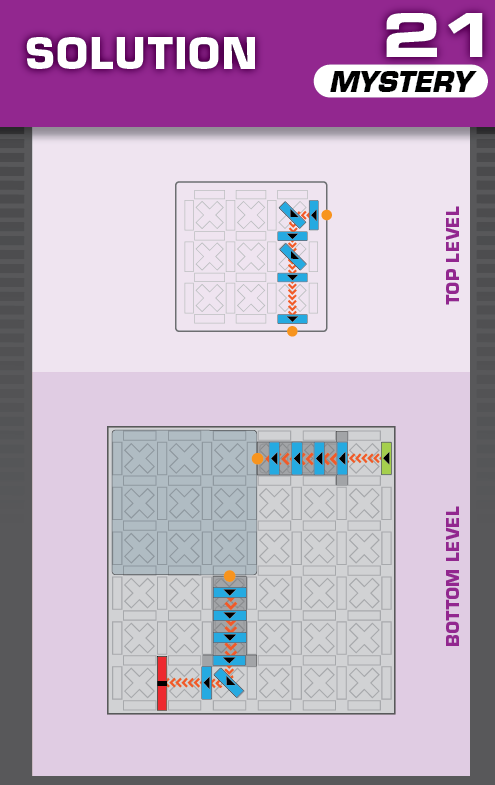 | V = 22 | 2 (unchanged) | ||
| The given solution is identical to the solution on published card 04. | (no solving notes) | ||||
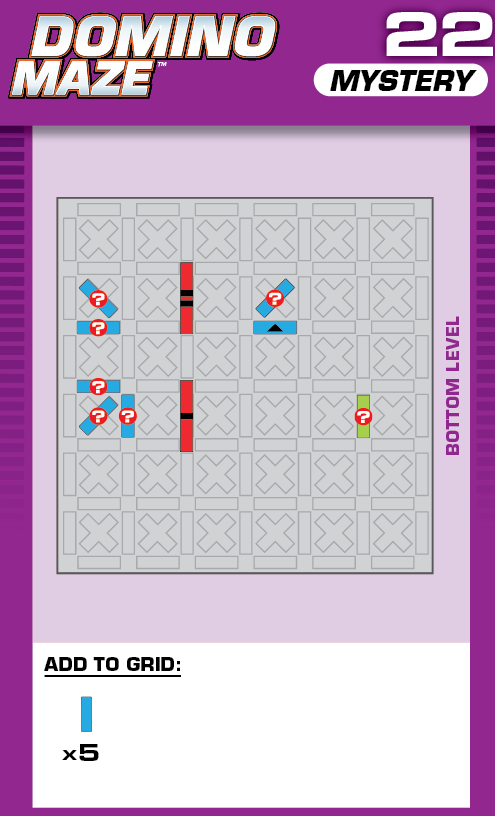 | 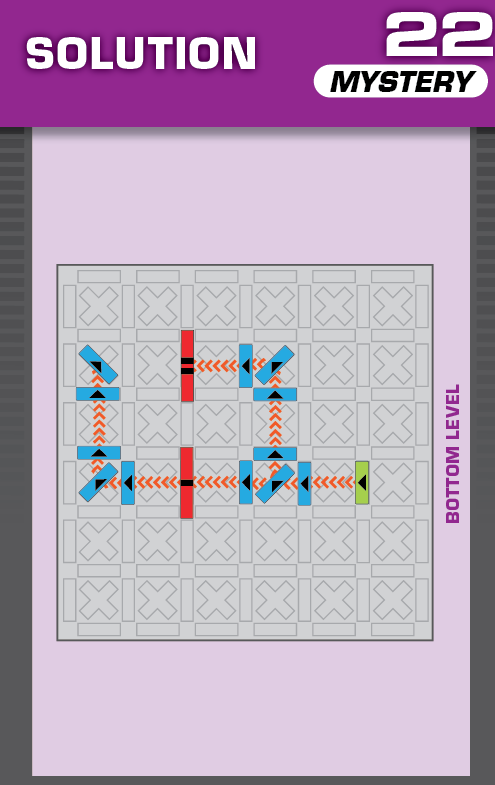 | A = 1 | 1 (unique) | 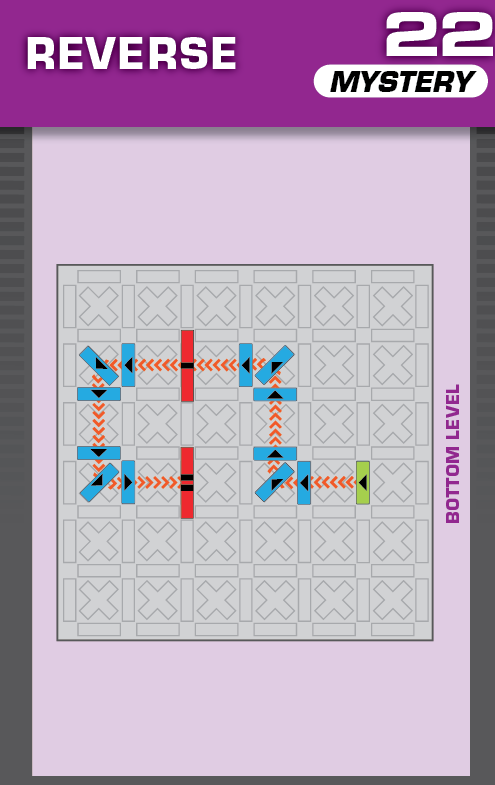 |
|
| (no solving notes) | (no solving notes) | ||||
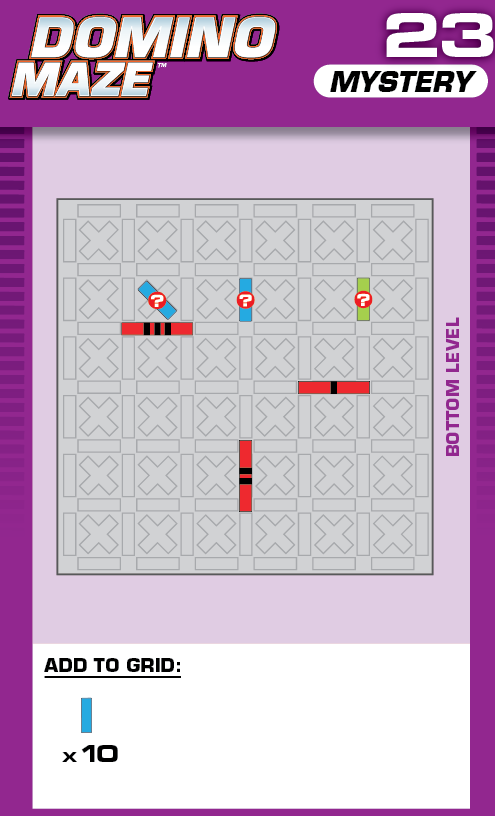 | 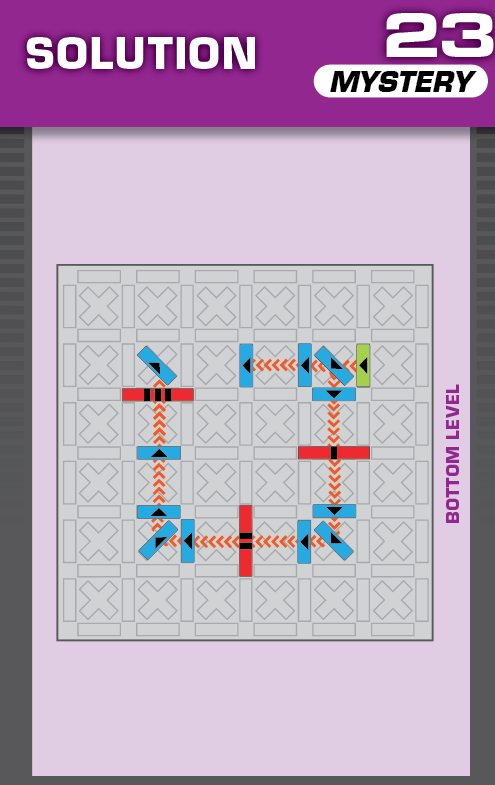 | B = 2 | (no solutions) | ||
| (no solving notes) | (no solving notes) | ||||
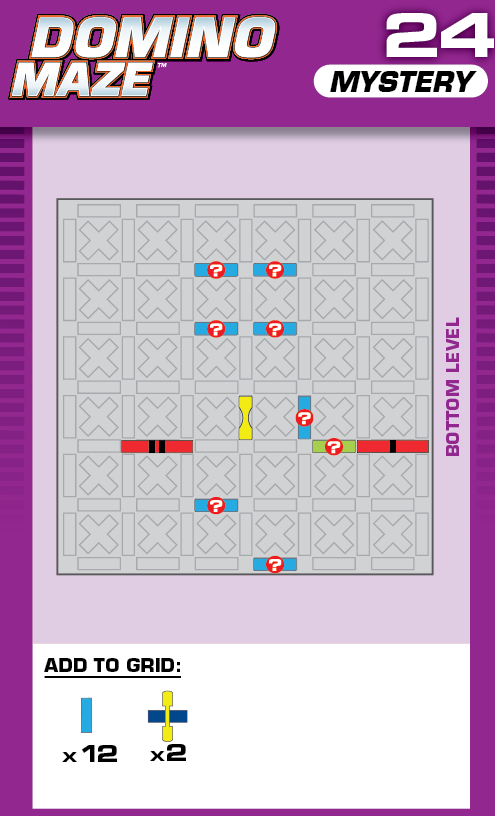 | 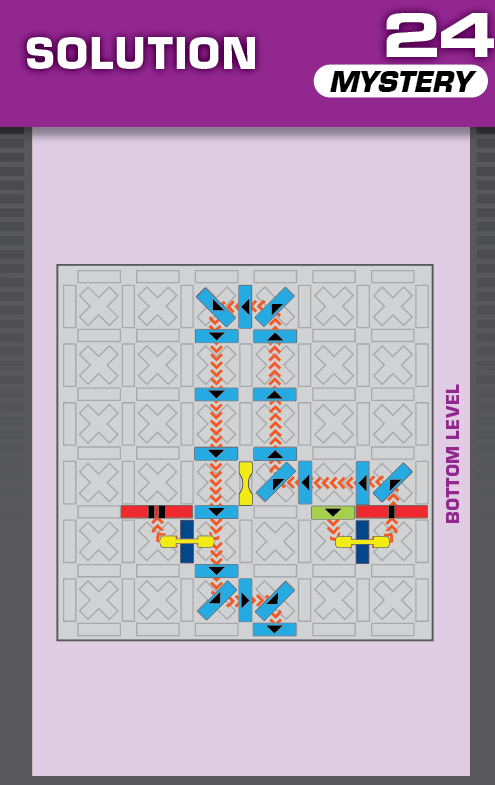 | L = 12 | 1 (unique) | 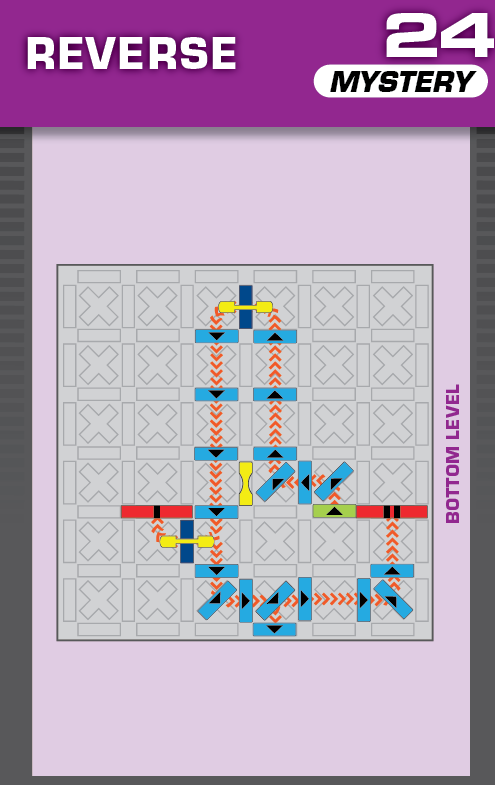 |
|
| (no solving notes) | (no solving notes) | ||||
 |
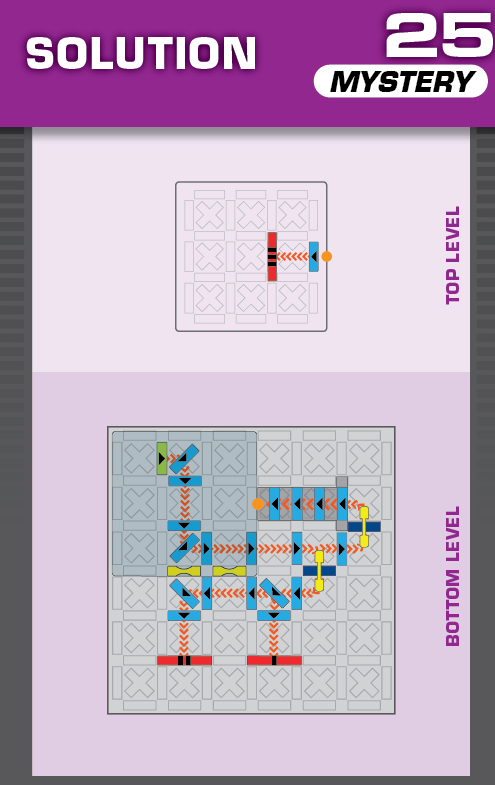 |
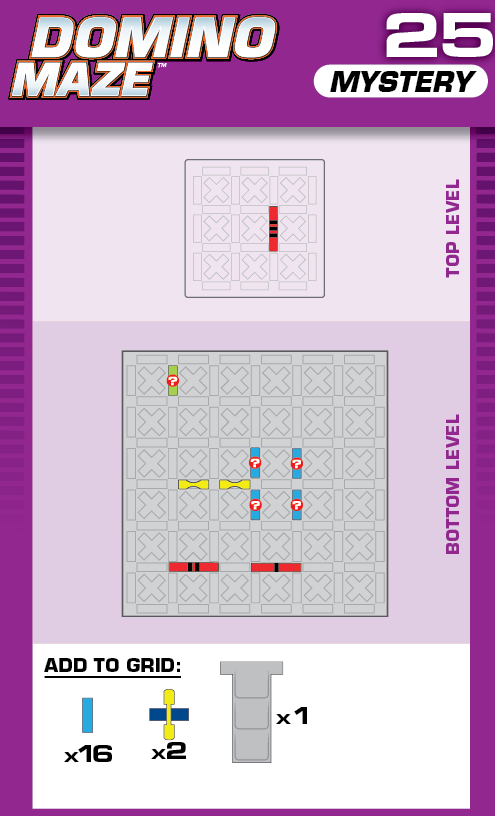
E = 5 | (no solutions) | ||
| This challenge is nearly identical to card 43 in the published deck, but the blocker arrangement is different. The changed blockers should help in determining the unprinted solution. | (no solving notes) | ||||
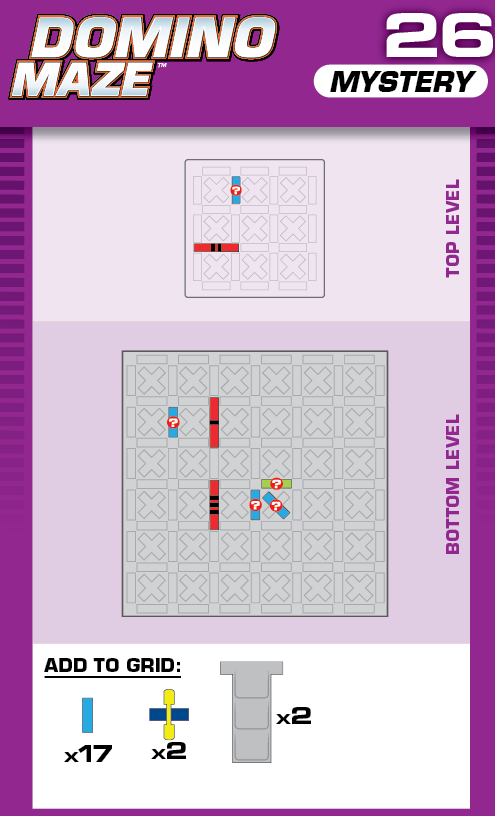 | 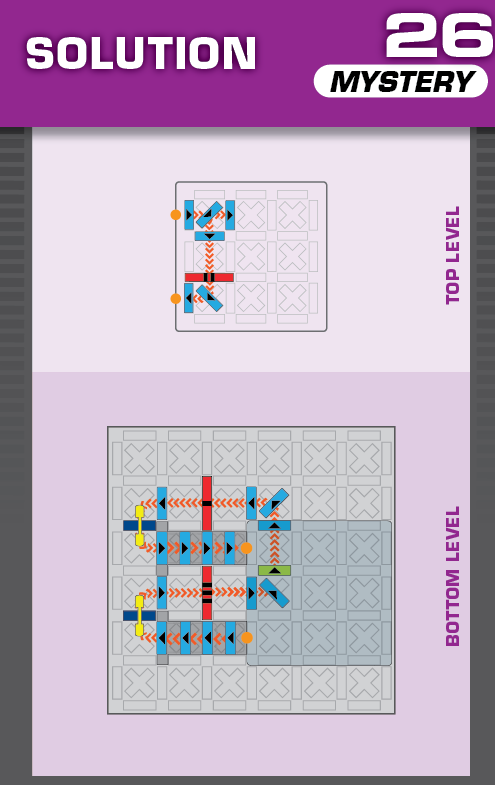 | W = 23 | 1 (unique) | 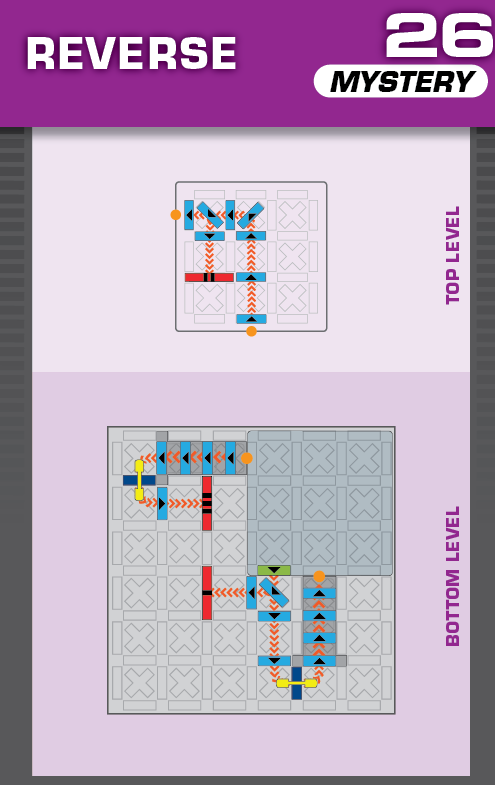 |
|
| (no solving notes) | (no solving notes) | ||||
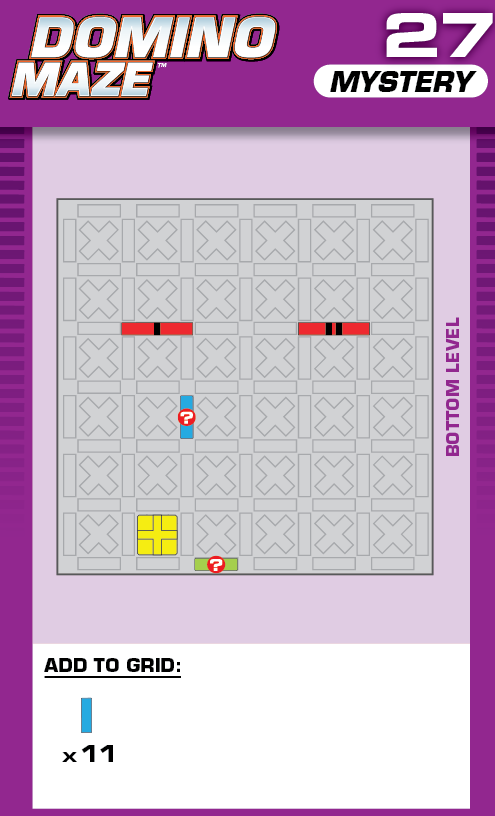 | 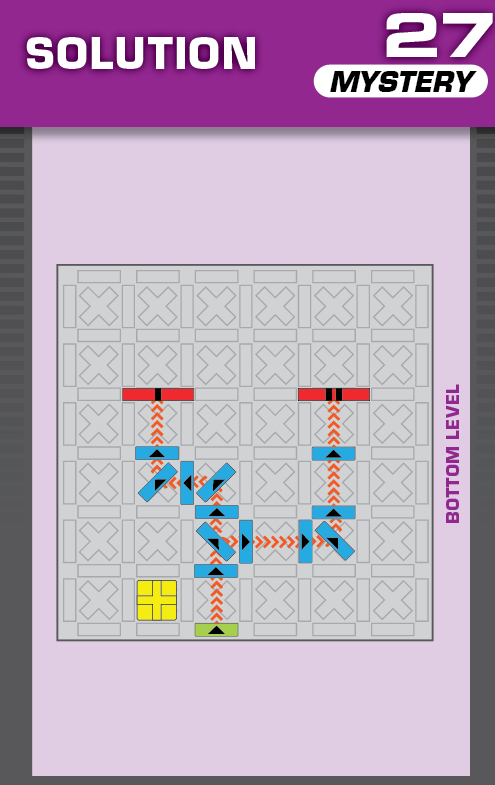 | I = 9 | (no solutions) | ||
| This challenge is somewhat reminiscent of card 12 in the published deck, but both the printed and unprinted solutions are different from the published deck. | (no solving notes) | ||||
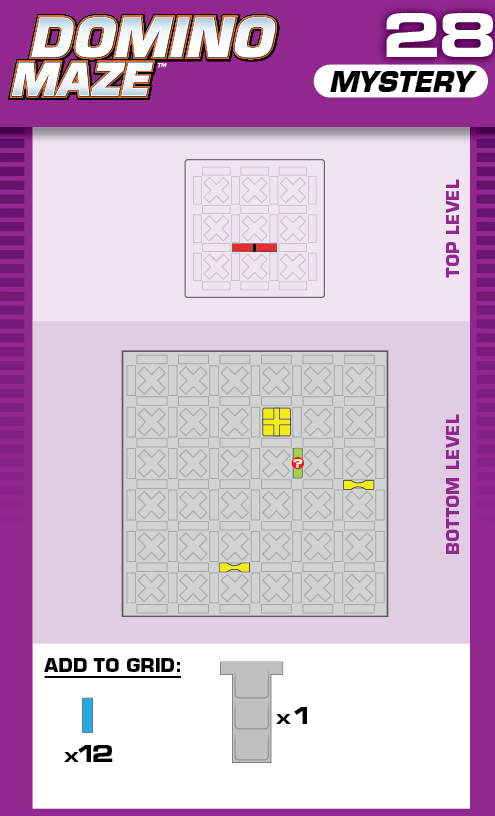 | 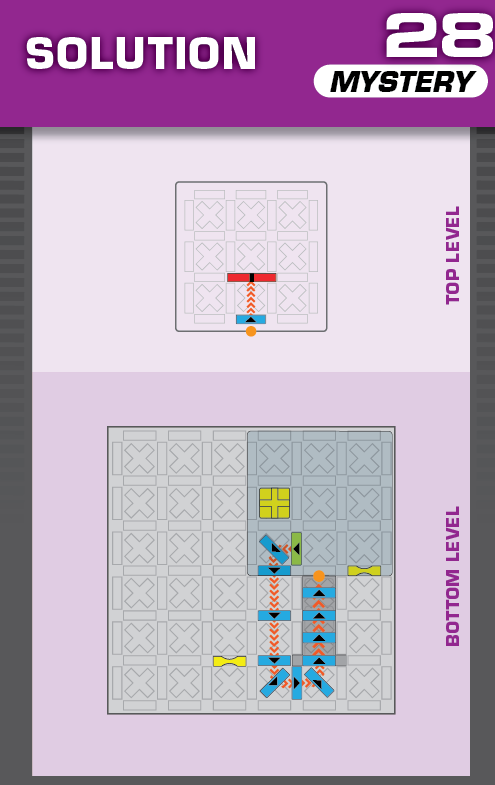 | T = 20 | 2 (unchanged) | ||
| (no solving notes) | (no solving notes) | ||||
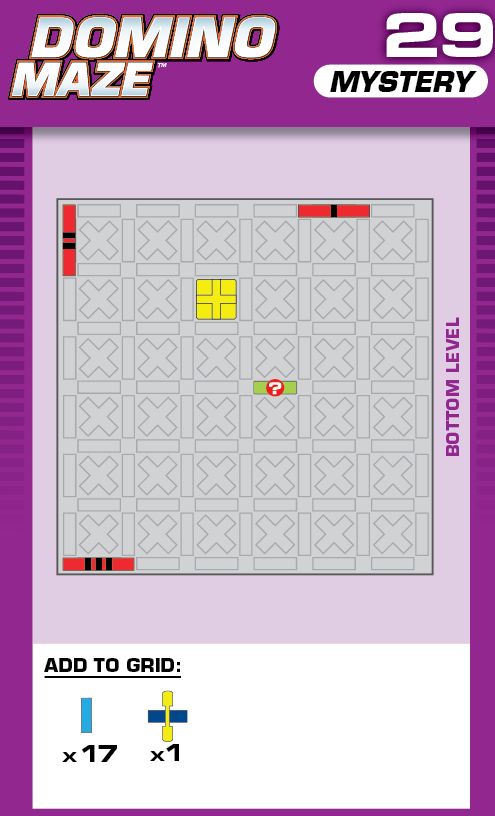 | 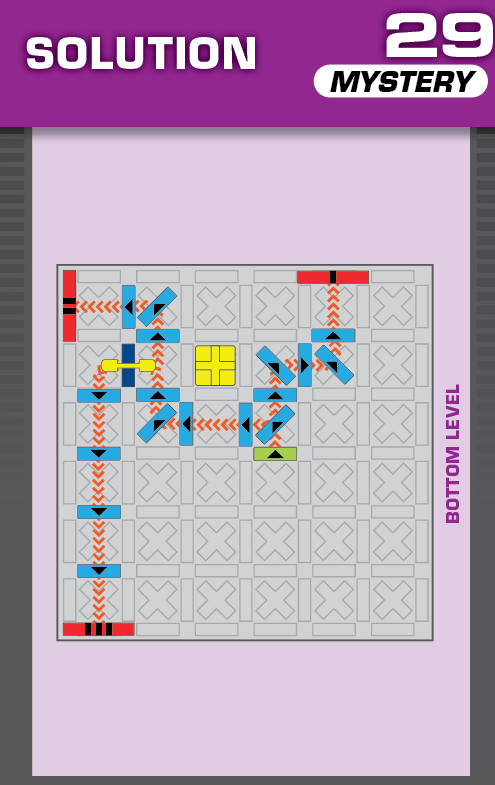 | H = 8 | (no solutions) | ||
| (no solving notes) | (no solving notes) | ||||
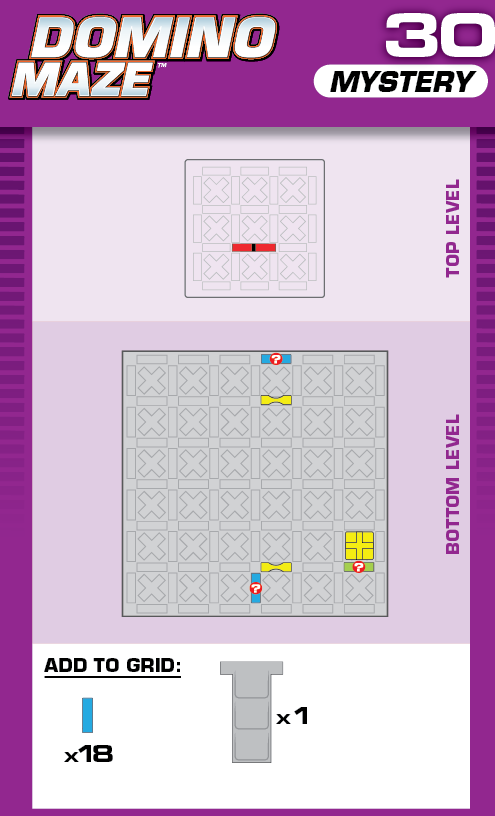 | 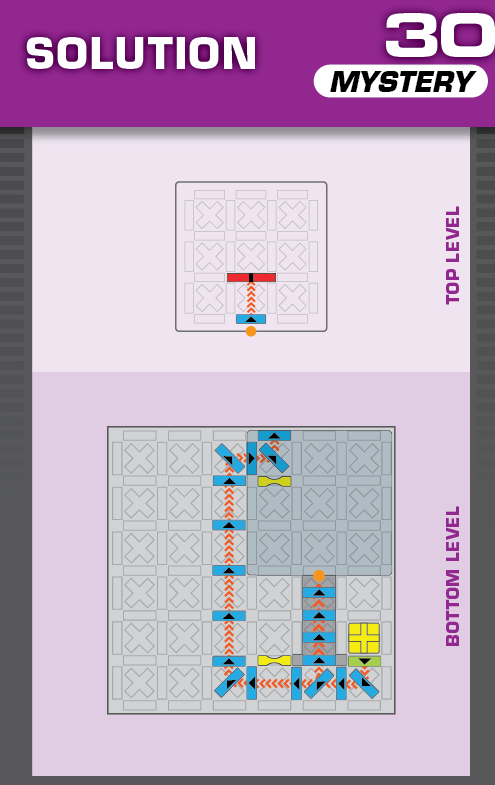 | R = 18 | 2 (unchanged) | ||
| (no solving notes) | (no solving notes) | ||||
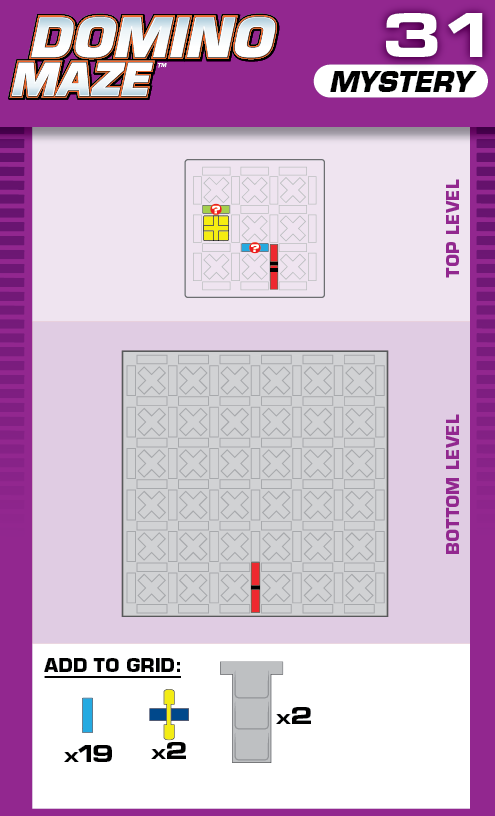 | 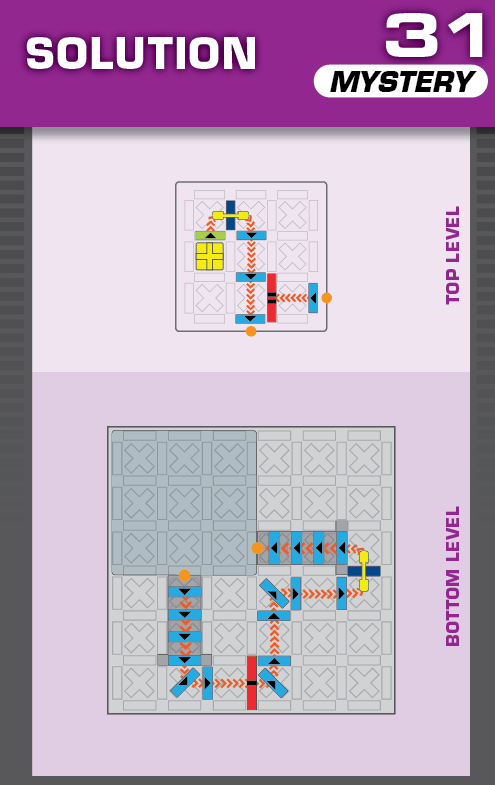 | E = 5 | more than 999 (9 unneeded dominoes and a stair) | 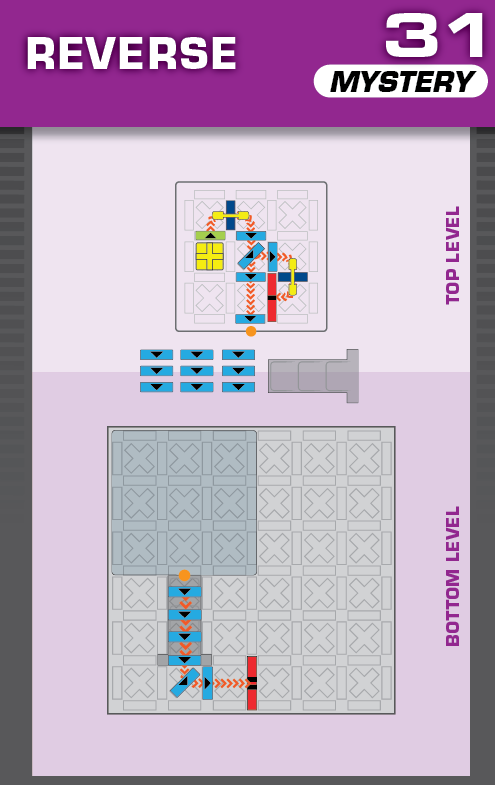 |
|
| (no solving notes) | (no solving notes) | ||||
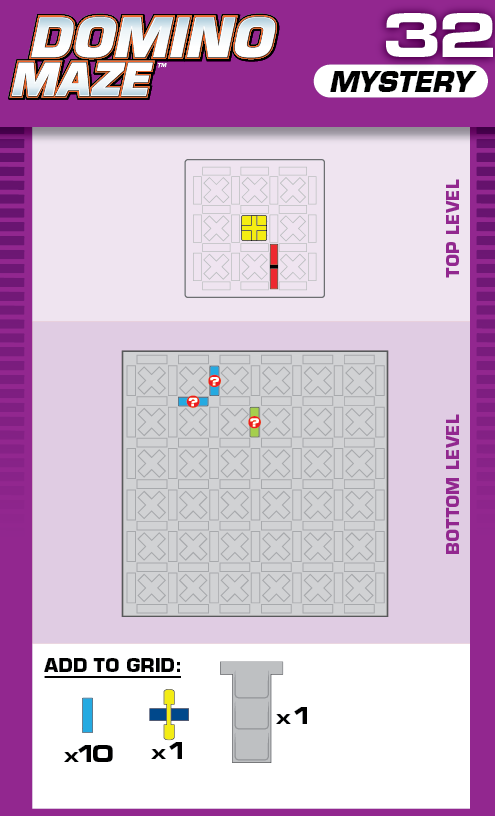 | 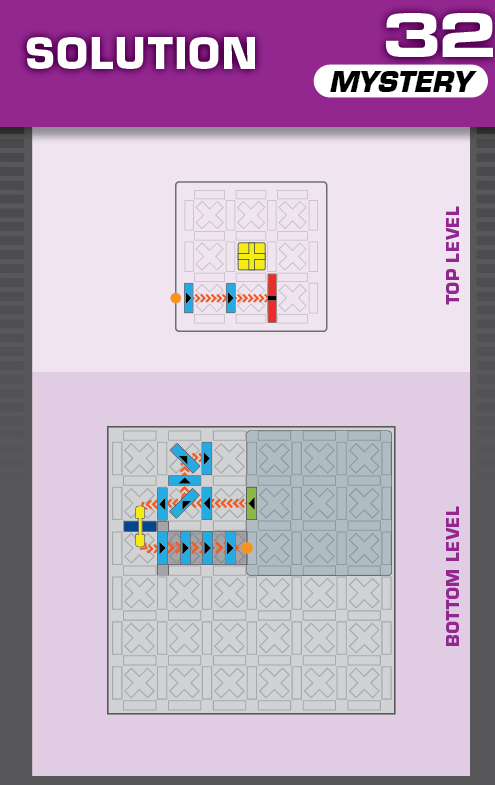 | V = 22 | 2 (unchanged) | ||
| This is nearly identical to challenge 14, with a reflection across the diagonal and one more blocker. | (no solving notes) | ||||
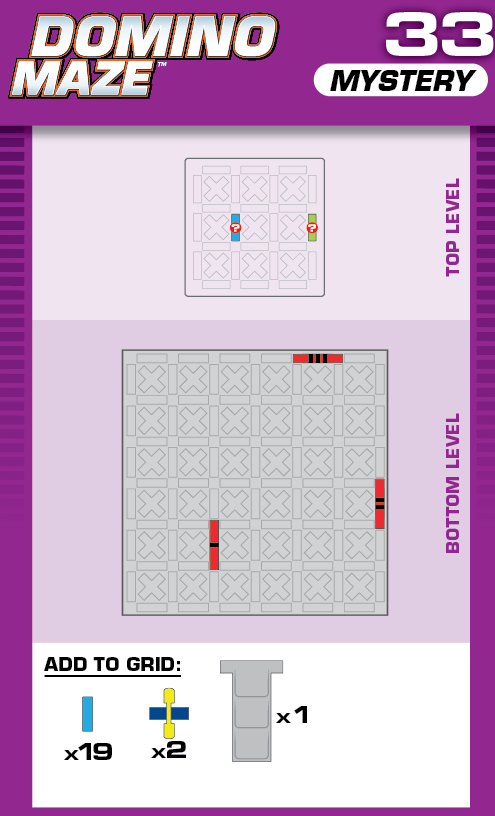 |  | E = 5 | (no solutions) | ||
| Because momentum changes direction rapidly, sometimes checkpoint 1 on the printed solution doesn't rise up all the way. The unprinted solution is fine. | (no solving notes) | ||||
 |  | R = 18 | 2 (unchanged) | ||
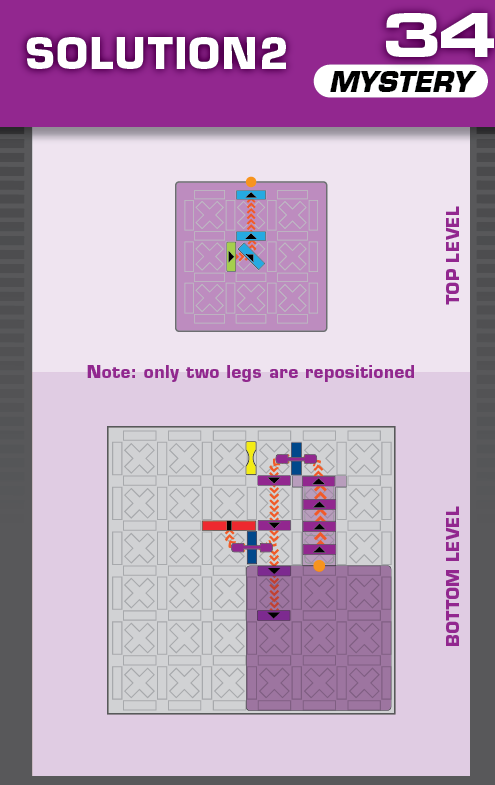
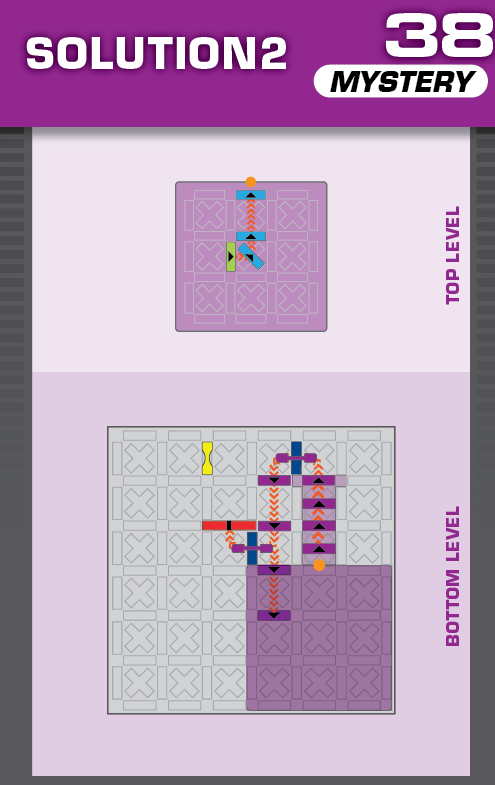
| Note that the unprinted solution is identical to the unprinted solution on challenge 38. | (no solving notes) | ||||
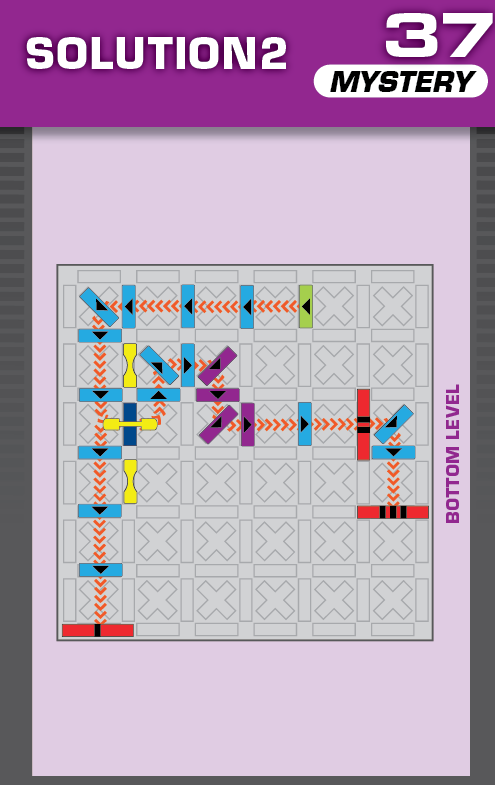
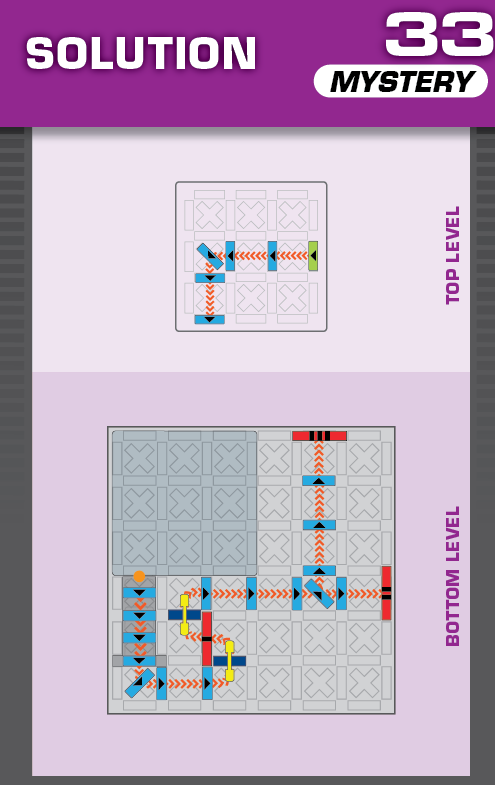
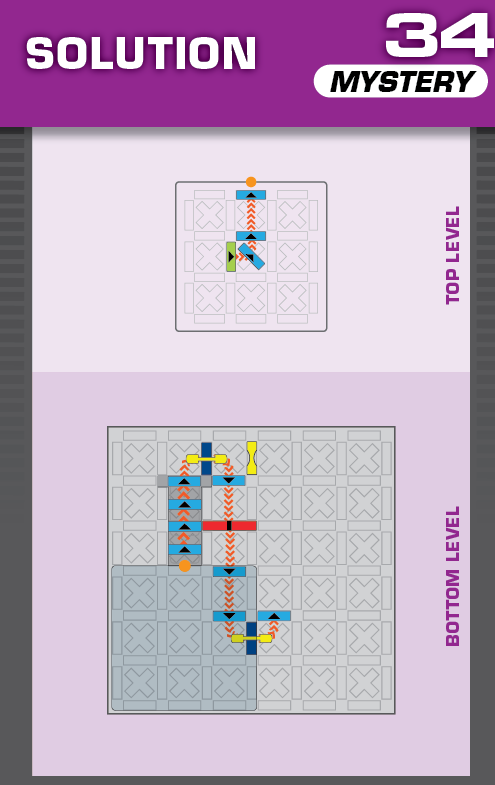
 | 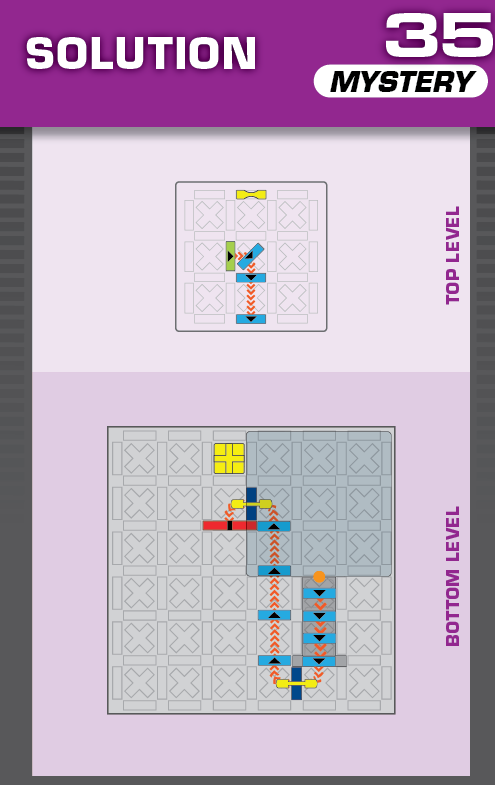 | S = 19 | 2 (unchanged) | ||
| While this arrangement is very similar to 34 and 38, both solutions are different from those. | (no solving notes) | ||||
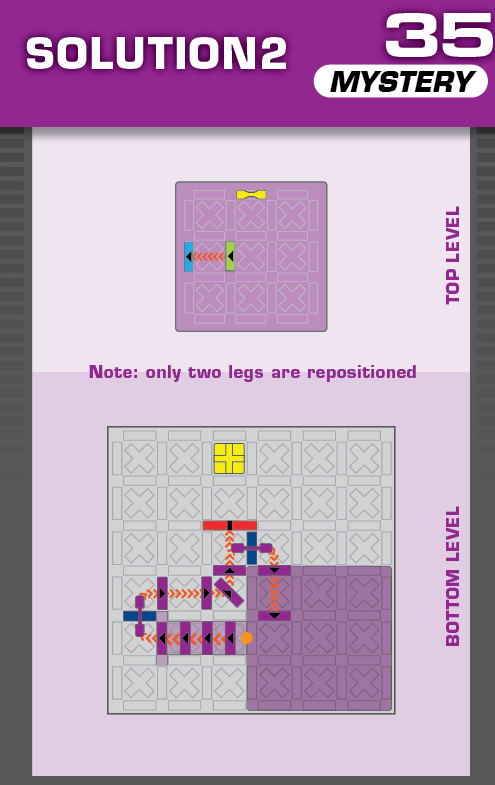
 | 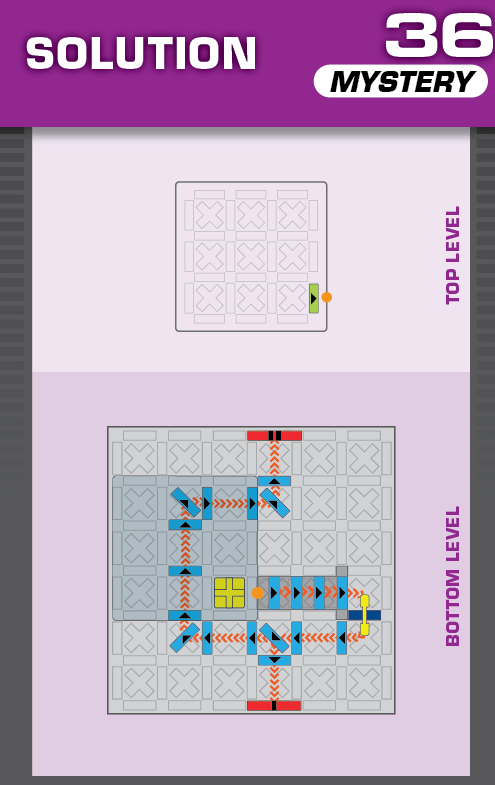 | E = 5 | 1 (unique) | 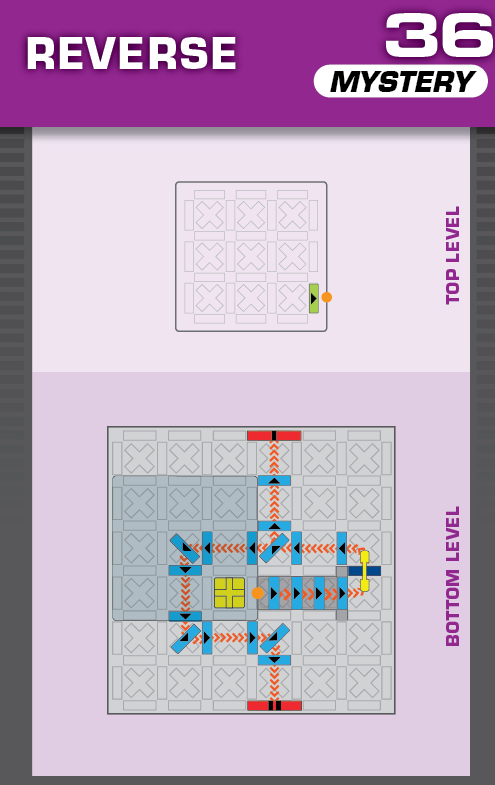 |
|
| (no solving notes) | (no solving notes) | ||||
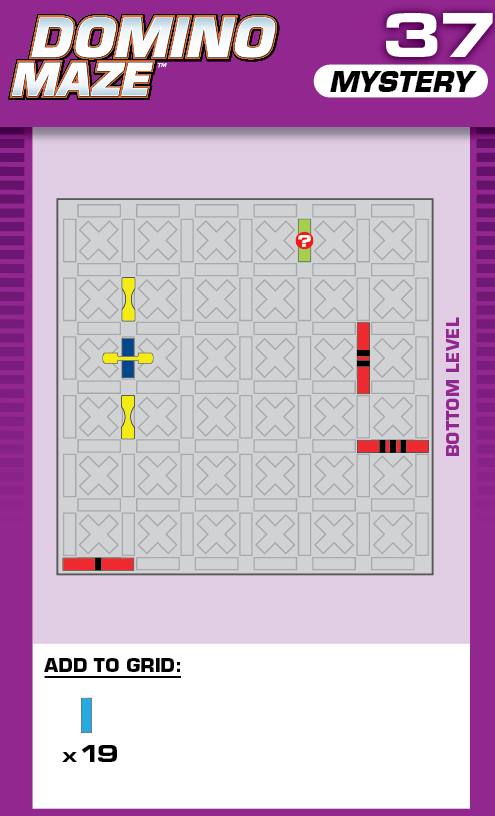 | 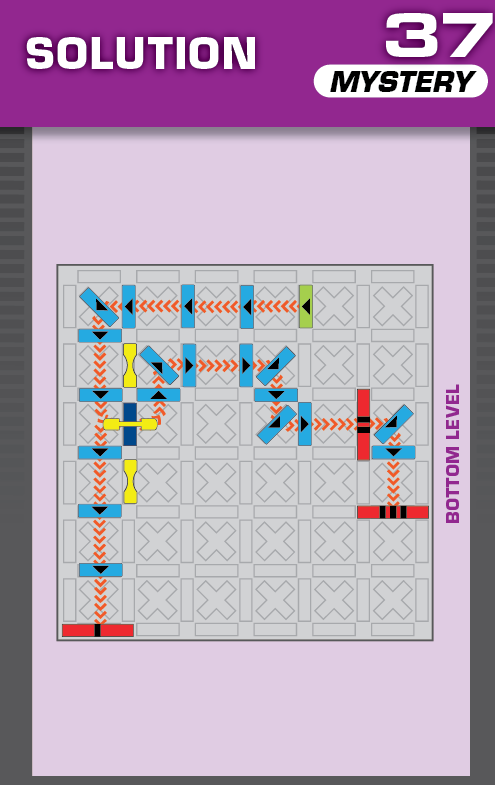 | D = 4 | (no solutions) | ||
| This challenge is very similar to 20 in the printed deck, but there's an added blocker and one less given domino. Those changes should hint towards what the unprinted solution is. | (no solving notes) | ||||
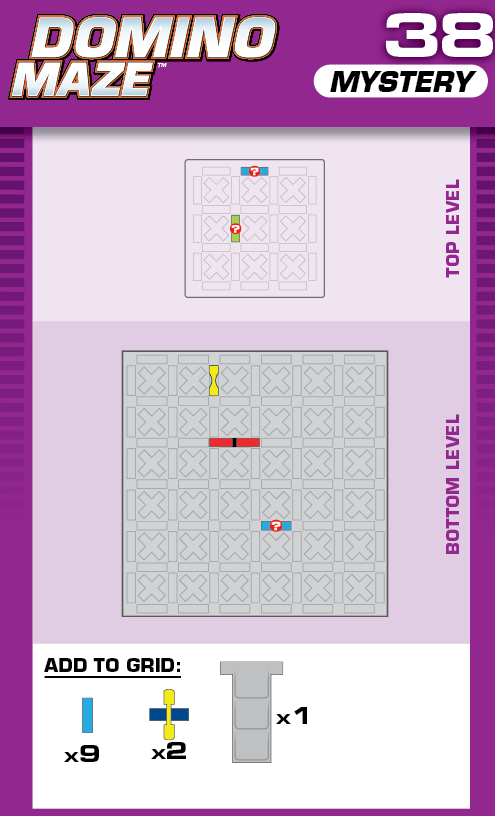 | 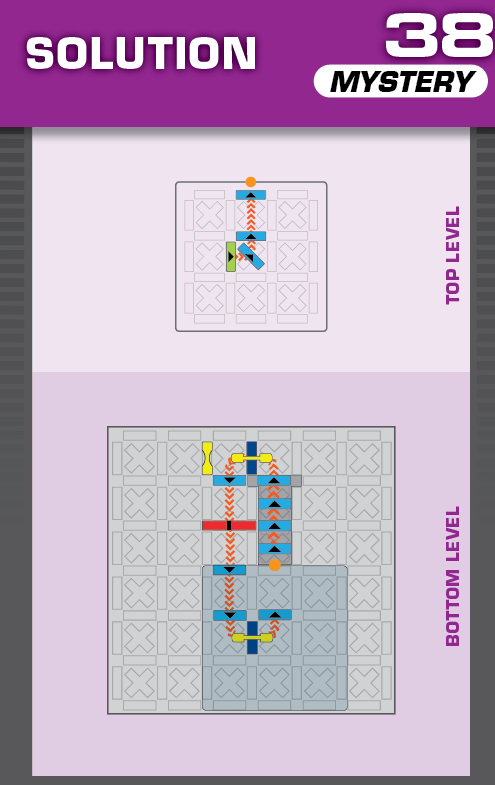 | T = 20 | 2 (unchanged) | ||
| Note that the unprinted solution is identical to the unprinted solution on challenge 34. | (no solving notes) | ||||
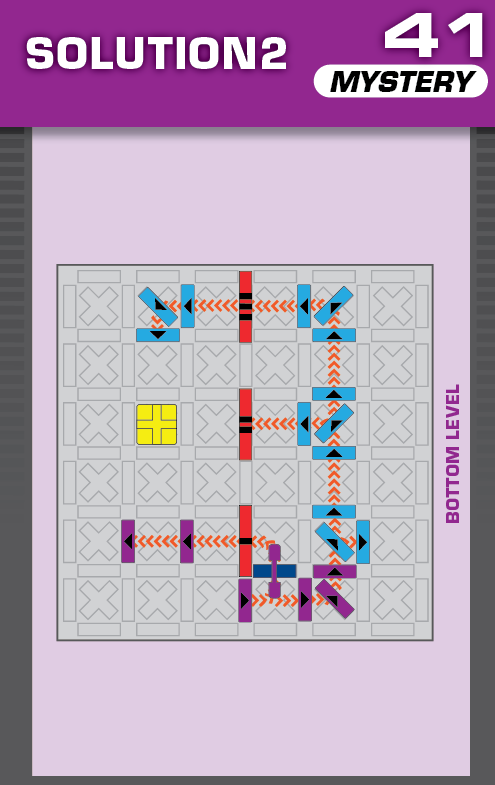
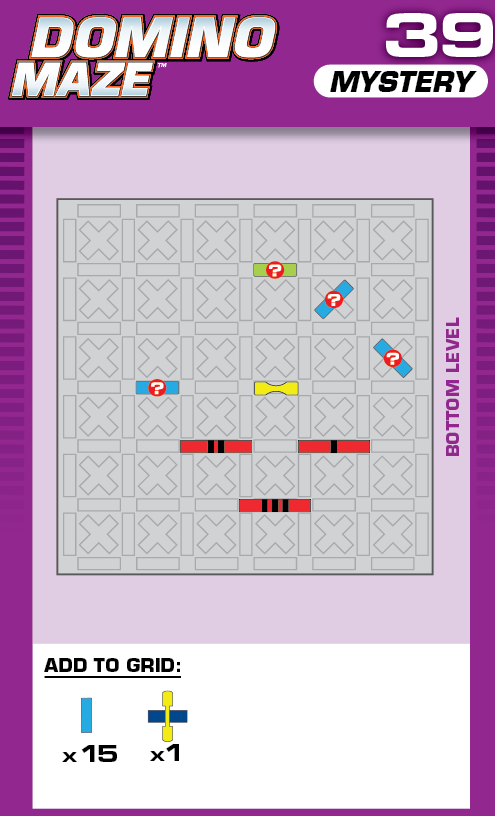 | 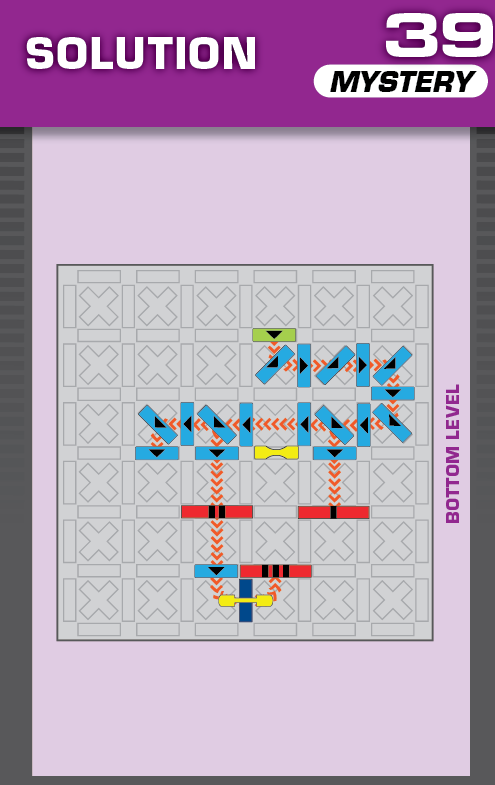 | A = 1 | (no solutions) | ||
| The unprinted solution is fine, but the printed solution will occasionally violate the rules. Sometimes the fourth domino to fall slides south and hits the tenth domino before the ninth domino can. This doesn't change the order in which the checkpoints get hit, but it means that the timing is occasionally earlier. | (no solving notes) | ||||
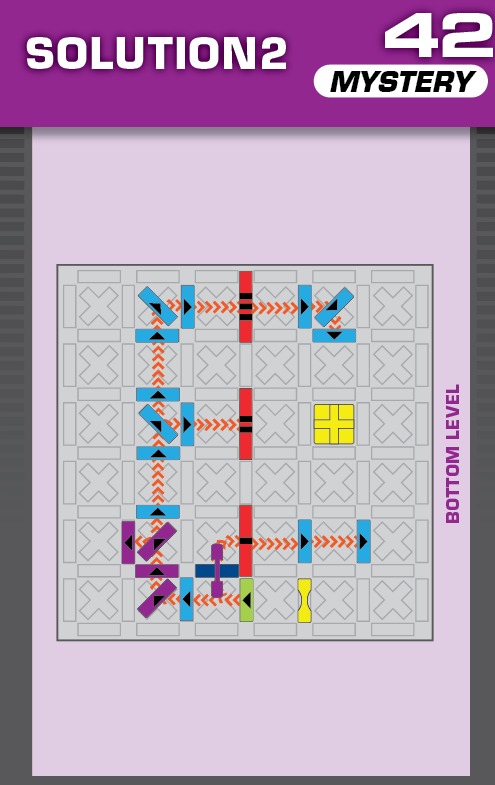
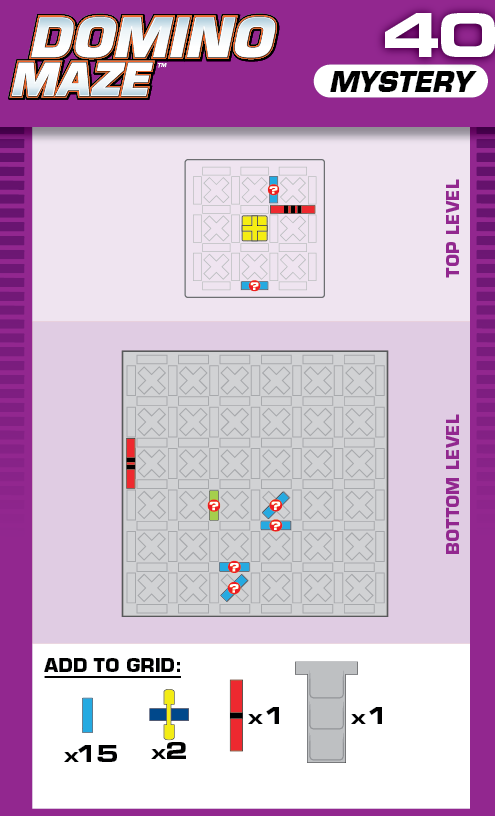 | 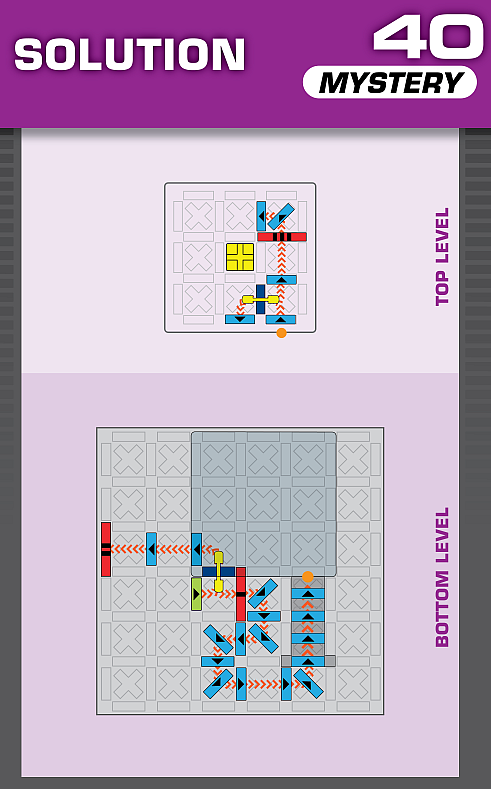 | R = 18 | (no solutions) | ||
| Note that the location of the first checkpoint is constrained by the location of the elevated grid, since it can't share a corner with one of the grid's supports. The unprinted solution works fine, but the printed solution sometimes doesn't have the checkpoint go up all the way because the domino after it doesn't get out of the way fast enough. | (no solving notes) | ||||
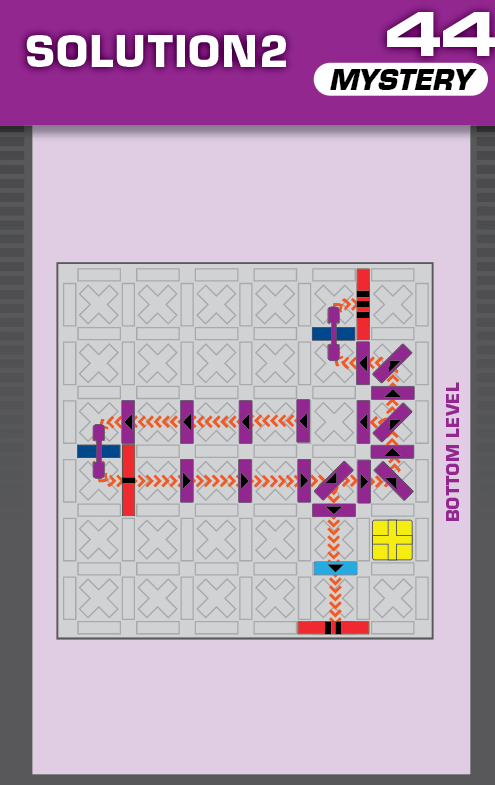
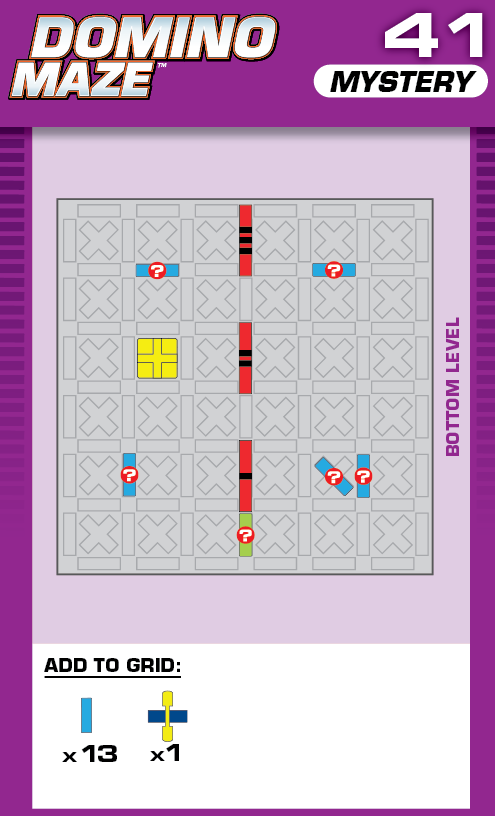 | 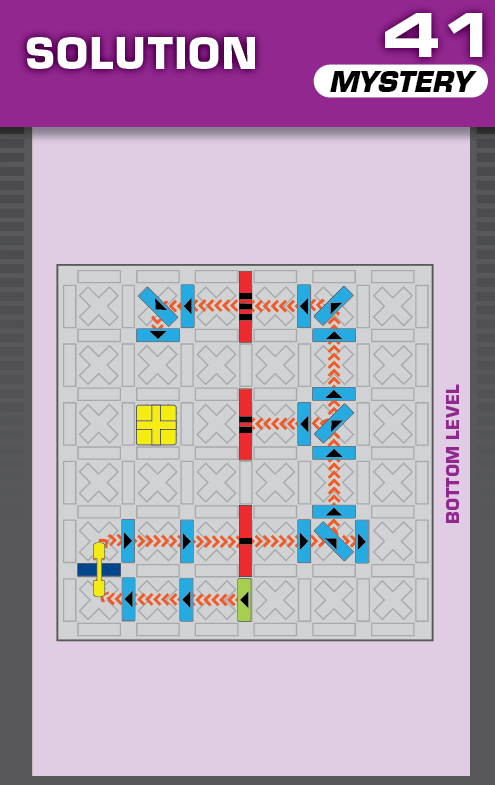 | G = 7 | (no solutions) | ||
| The unprinted solution is a simple reflection of that of challenge 42. | (no solving notes) | ||||
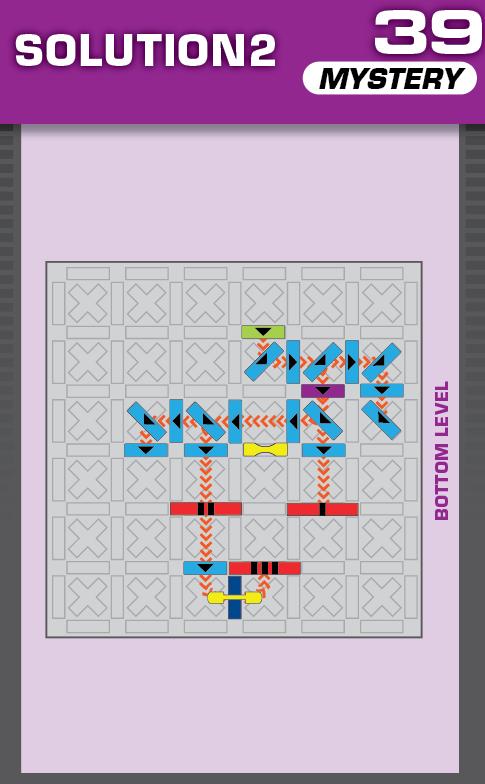
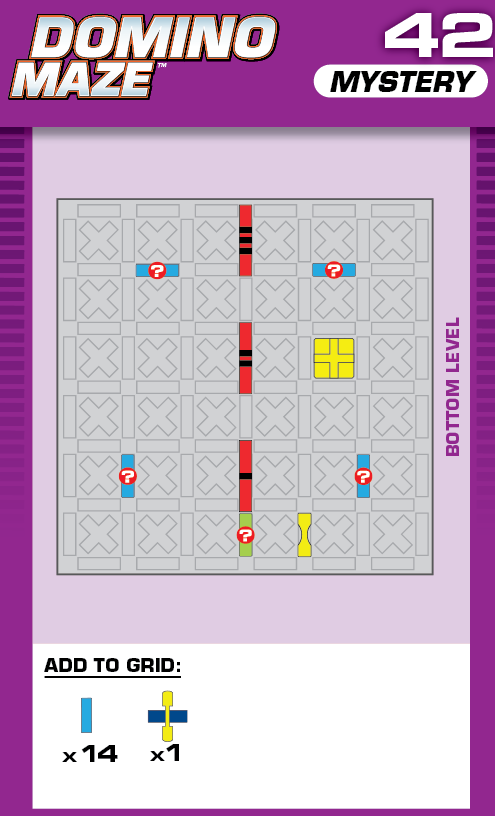 | 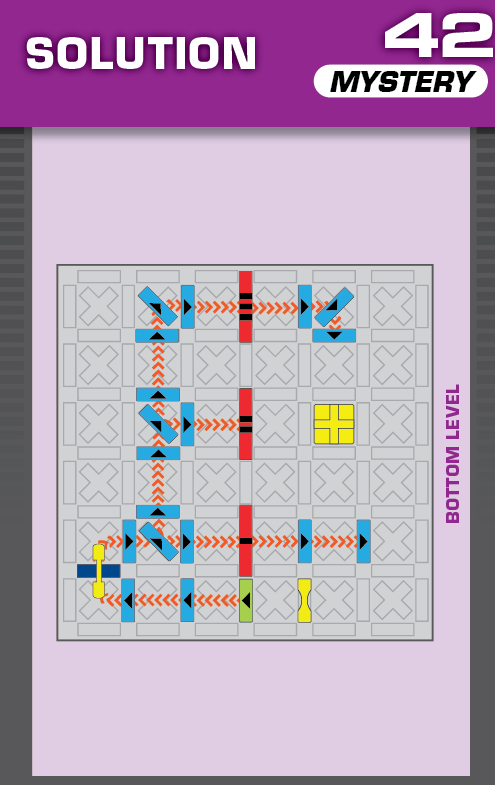 | E = 5 | (no solutions) | ||
| The unprinted solution is a simple reflection of that of challenge 41. | (no solving notes) | ||||
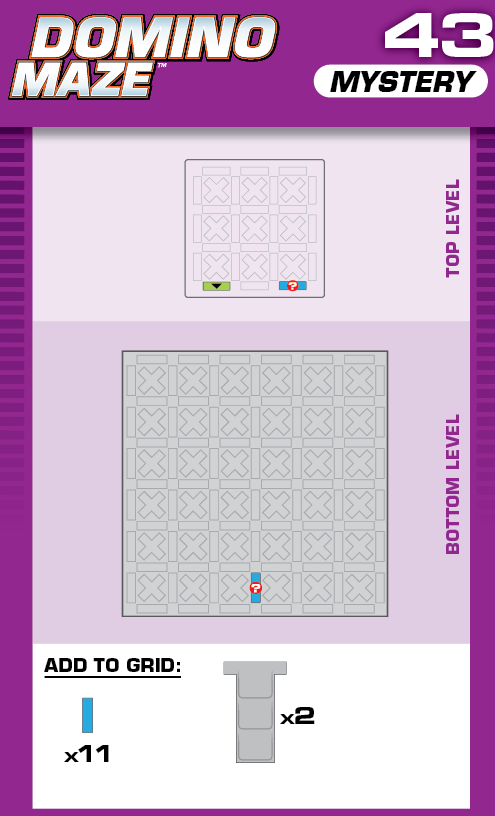 | 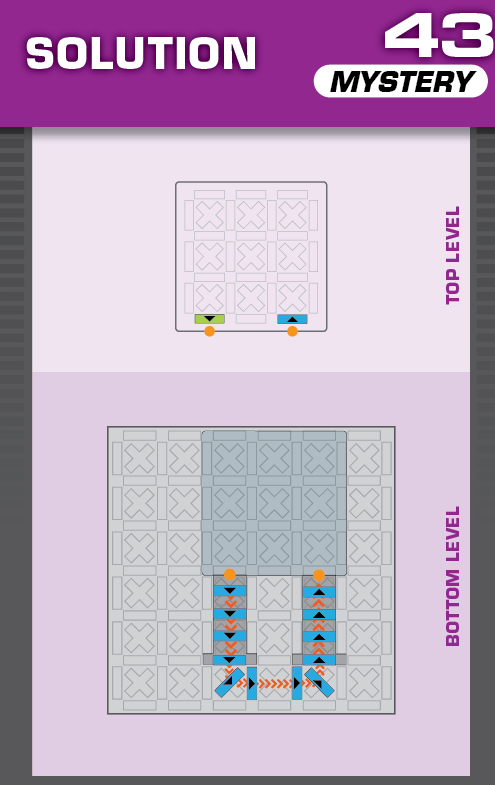 | T = 20 | 2 (unchanged) | ||
| (no solving notes) | (no solving notes) | ||||
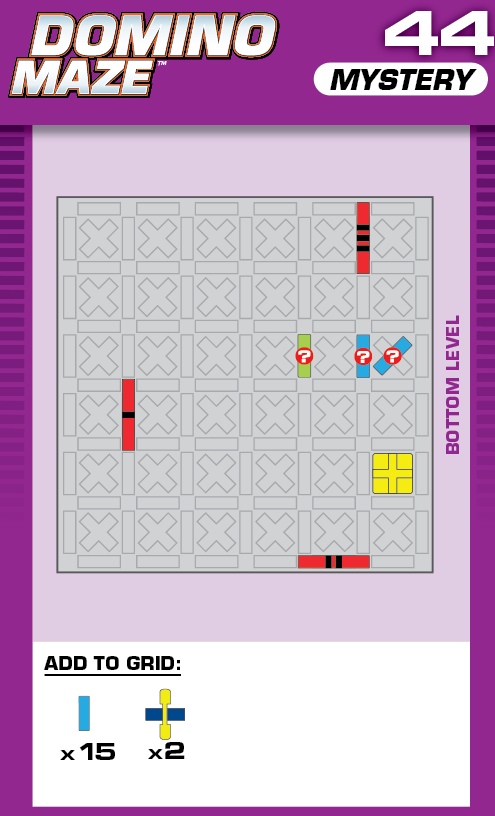 | 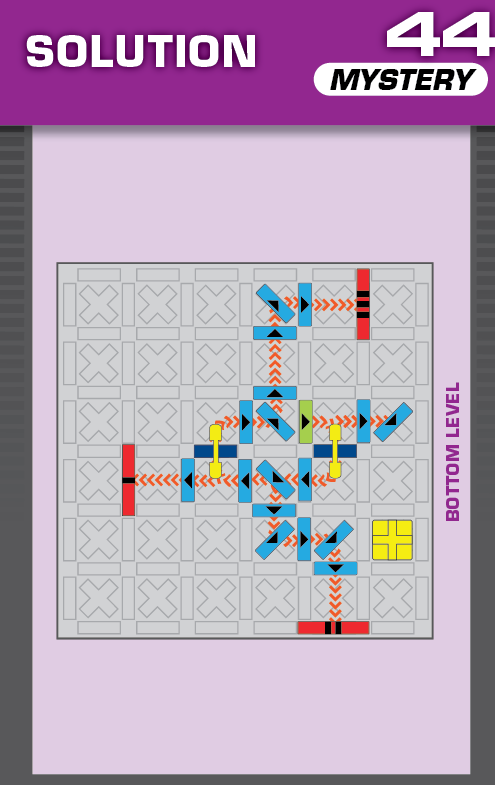 | S = 19 | more than 999 (4 unneeded dominoes) | 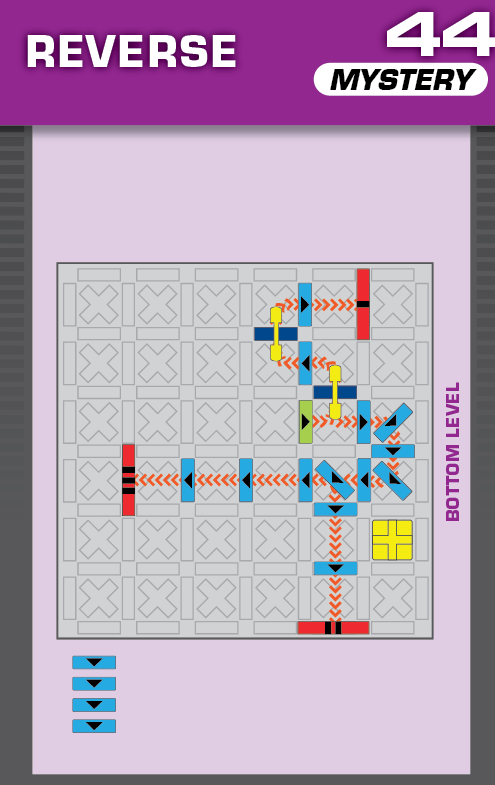 |
|
| (no solving notes) | (no solving notes) |