Solution to Scrambling Attributes Yields Conundrum
by Cat Miller and Reid Barton
These are bridge hands whose suits and values are obfuscated. The title
clues that the bidding system used is standard SAYC.
The first step is to determine suits.  = NT and
= NT and
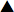 = Clubs are determinable by the consecutive
bidding at a given suit level.
= Clubs are determinable by the consecutive
bidding at a given suit level. 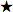 is forced to be Spades because
in board 3 West bids a transfer over NT to
is forced to be Spades because
in board 3 West bids a transfer over NT to 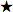 . If
. If 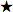 were Hearts and
were Hearts and  were Spades then West's correct bidding under
SAYC would be to bid Stayman. (The SAYC way to bid the hands if the suits are SHDC in order
is 1NT—2C—2D—2H (invite with 5H 4S)—pass.) Since instead West
bids a transfer, it must be the case that
were Spades then West's correct bidding under
SAYC would be to bid Stayman. (The SAYC way to bid the hands if the suits are SHDC in order
is 1NT—2C—2D—2H (invite with 5H 4S)—pass.) Since instead West
bids a transfer, it must be the case that 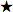 = Spades,
= Spades,
 = Hearts, and thus
= Hearts, and thus  = Diamonds.
= Diamonds.
It is now possible to solve for the high cards as a logic puzzle using SAYC bidding rules.
(Note there is no way to solve for the spot cards.)
The unscrambled hands are shown below. For each hand, add up the high card points
and convert to letters via A=1, B=2 to get THE PI OF STARS, which in obfuscated-land is
THE QUEEN OF SPADES.
1.
West
♦ K Q 5 2
♠ A 10
♥ K 7 J
♣ 7 A Q J
East
♦ 9 3
♠ K 7 3 8
♥ 8 Q 2
♣ K 9 8 10
West
2 NT
3 ♦
| North
pass
pass
| East
3 ♣
3 NT
| South
pass
All pass
|
2.
West
♦ 8 2 6
♠ 4 Q 2 6 J
♥ —
♣ 7 3 Q 2 6
East
♦ 3 Q J
♠ A 10
♥ 4 A 10 J
♣ 4 A 10 5
West
2 ♥
| North
pass
pass
| East
1 NT
2 ♠
| South
pass
All pass
|
3.
West
♦ 4 8 5 6
♠ 4 9 3 8 A
♥ 9 J
♣ A 2
East
♦ 9 J
♠ K Q J
♥ 8 Q 5 6
♣ K 4 Q J
West
2 ♥
2 NT
| North
pass
pass
pass
| East
1 NT
2 ♠
3 ♠
| South
pass
pass
All pass
|
4.
West
♦ 4 6 J
♠ 4 9 3 8 6
♥ 7 4 A 6
♣ J
East
♦ 3 A 5
♠ K 7 A Q 5
♥ Q J
♣ K 4 5
West
4 ♠
| North
pass
All pass
| East
1 ♠
| South
pass
|
5.
West
♦ K 3 8 A Q 10 2
♠ 8 A
♥ K Q
♣ Q 2
East
♦ 6
♠ 7 2 6
♥ 9 3 5 6
♣ 9 8 5 6 J
West
1 ♦
| North
All pass
| East
| South
|
6.
West
♦ K A J
♠ 3 J
♥ K 3 A 6
♣ 7 4 3 Q
East
♦ 9 8 Q
♠ K 4 9 A Q
♥ 5 J
♣ K 8 A
West
1 ♣
2 NT
| North
pass
pass
| East
1 ♠
7 NT
| South
pass
All pass
|
 = NT and
= NT and
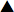 = Clubs are determinable by the consecutive
bidding at a given suit level.
= Clubs are determinable by the consecutive
bidding at a given suit level. 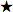 is forced to be Spades because
in board 3 West bids a transfer over NT to
is forced to be Spades because
in board 3 West bids a transfer over NT to 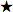 . If
. If 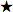 were Hearts and
were Hearts and  were Spades then West's correct bidding under
SAYC would be to bid Stayman. (The SAYC way to bid the hands if the suits are SHDC in order
is 1NT—2C—2D—2H (invite with 5H 4S)—pass.) Since instead West
bids a transfer, it must be the case that
were Spades then West's correct bidding under
SAYC would be to bid Stayman. (The SAYC way to bid the hands if the suits are SHDC in order
is 1NT—2C—2D—2H (invite with 5H 4S)—pass.) Since instead West
bids a transfer, it must be the case that 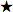 = Spades,
= Spades,
 = Hearts, and thus
= Hearts, and thus  = Diamonds.
= Diamonds.